搜索
【题目】如图，纸上有五个边长为1的小正方形组成的图形纸（图1），我们可以把它剪开拼成一个正方形（图2）．
（1）图2中拼成的正方形的面积是 _________ ；边长是 _________ ；（填实数）
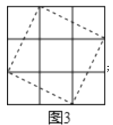
（2）请你在图3中画一个面积为5的正方形，要求所画正方形的顶点都在格点上．请用虚线画出．
（3）你能把十个小正方形组成的图形纸（图4），剪开并拼成正方形吗？若能，请仿照图2的形式把它重新拼成一个正方形．并求出它的边长．
参考答案：
【答案】（1）5，
；（2）详情见解析；（3）能，详情见解析，边长为
.
【解析】
（1）根据正方形的面积求出边长即可.
（2）根据正方形面积求出边长，再利用勾股定理作出正方形即可.
（3）根据勾股定理作出边长为的边，并剪出两个直角三角形，然后拼接成正方形即可.
（1）∵正方形面积仍然为5
∴边长为
（2）如图所示：
（3）如图所示：
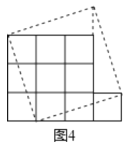
其边长为.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负.如果从A到B记为：A→B(+1，+4)，从B到A记为：B→A(-1，-4)，其中第一个数表示左右方向，第二个数表示上下方向．
（1）图中A→C( ， )，B→C( ， )，C→ (+1， )；
（2）若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，-1），（-2，+3），（-1，-2），请在图中标出P的位置；
（3）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（4）若图中另有两个格点M、N，且M→A（3-a，b-4），M→N（5-a，b-2），则N→A应记为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C为∠AOB的边OA上一点，OC＝6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M．
（1）若∠AOB＝60，OM＝4，OQ＝1，求证：CN⊥OB．
（2）当点N在边OB上运动时，四边形OMPQ始终保持为菱形．
①问：
的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．
②设菱形OMPQ的面积为S1，△NOC的面积为S2，求
的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】A、B、C、D四个车站的位置如图所示，A、B两站之间的距离AB＝a﹣b，B、C两站之间的距离BC＝2a﹣b，B、D两站之间的距离BD＝
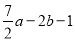．(1)求A、C两站之间的距离AC.
(2)若A、C两站之间的距离AC＝90km，求C、D两站之间的距离CD．
-
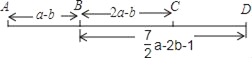
科目： 来源： 题型：
查看答案和解析>>【题目】数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片边长为a的正方形，B种纸片是边长为b的正方形，C种纸片长为a、宽为b的长方形．并用A种纸片一张，B种纸片张，C种纸片两张拼成如图2的大正方形．
（1）请用两种不同的方法求图2大正方形的面积．
方法1： ；方法2：
（2）观察图2，请你写出下列三个代数式：（a+b）2，a2+b2，ab之间的等量关系．
（3）根据（2）题中的等量关系，解决如下问题：
①已知：a+b=5，a2+b2=11，求ab的值；
②已知（2018﹣a）2+（a﹣2017）2=5，求（2018﹣a）（a﹣2017）的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，AD是△ABC的中线，将BC边所在直线绕点D顺时针旋转
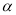角，交边AB于点M，交射线AC于点N，设AM=xAB，AN=yAC(x,y≠0).（1）如图1，当△
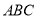为等边三角形且
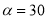°时，证明：△AMN∽△DMA；（2）如图2，证明：
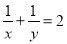；（3）如图3，当G是AD上任意一点时（点G不与A重合），过点G的直线交边AB于点
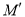，交射线AC于点
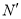，设AG=nAD， 
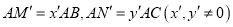，猜想：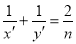 
是否成立？并说明理由.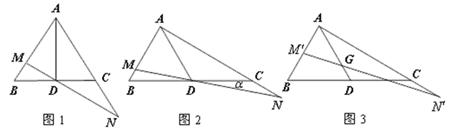
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，矩形ABCD的边AD在y轴上，抛物线
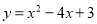经过点A、点B，与x轴交于点E、点F，且其顶点M在CD上。（1）请直接写出下列各点的坐标：
A ，B ，C ，D ；
（2）若点P是抛物线上一动点（点P不与点A、点B重合），过点P作
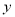轴的平行线l与直线AB交于点G，与直线BD交于点H，如图2。①当线段PH=2GH时，求点P的坐标；
②当点P在直线BD下方时，点K在直线BD上，且满足△KPH∽△AEF，求△KPH面积的最大值。
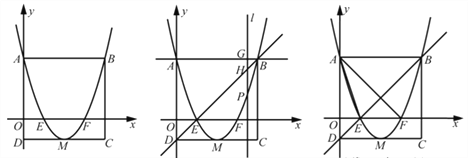
图1 图2 备用图
相关试题
