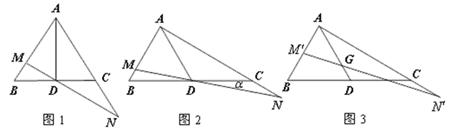
【题目】已知,AD是△ABC的中线,将BC边所在直线绕点D顺时针旋转![]() 角,交边AB于点M,交射线AC于点N,设AM=xAB,AN=yAC(x,y≠0).
角,交边AB于点M,交射线AC于点N,设AM=xAB,AN=yAC(x,y≠0).
(1)如图1,当△![]() 为等边三角形且
为等边三角形且![]() °时,证明:△AMN∽△DMA;
°时,证明:△AMN∽△DMA;
(2)如图2,证明: ![]() ;
;
(3)如图3,当G是AD上任意一点时(点G不与A重合),过点G的直线交边AB于点![]() ,交射线AC于点
,交射线AC于点![]() ,设AG=nAD,
,设AG=nAD, ![]() ,猜想:
,猜想: ![]() 是否成立?并说明理由.
是否成立?并说明理由.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)猜想成立,理由见解析.
【解析】试题分析:(1)利用“两角法”证得两个三角形相似;
(2)如图1,过点C作CF∥AB交MN于点F,构建相似三角形:△CFN∽△AMN,利用该相似三角形的对应边成比例求得![]() .通过证△CFD≌△BMD得到BM=CF,利用比例的性质和相关线段的代入得到
.通过证△CFD≌△BMD得到BM=CF,利用比例的性质和相关线段的代入得到![]() ,即
,即![]() ;
;
(3)猜想: ![]() +
+![]() =
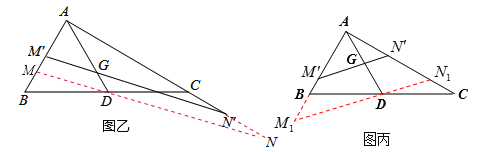
=![]() 成立.需要分类讨论:①如图乙,过D作MN∥M'N'交AB于M,交AC的延长线于N.由平行线截线段成比例得到
成立.需要分类讨论:①如图乙,过D作MN∥M'N'交AB于M,交AC的延长线于N.由平行线截线段成比例得到![]() ,易求
,易求![]() ,利用(2)的结果可以求得
,利用(2)的结果可以求得![]() ;
;
②如图丙,当过点D作M1N1∥M'N'交AB的延长线于M1,交AC1于N1,则同理可得![]() .
.
试题解析:解:(1)证明:如图1.在△AMD中,∵AD是△ABC的中线,△ABC为等边三角形,∴AD⊥BC,∠MAD=30°.又∵α=∠BDM=30°,∴∠MDA=60°,∴∠AMD=90°.在△AMN中,∠AMN=90°,∠MAN=60°,∴∠AMN=∠DMA=90°,∠MAN=∠MDA,∴△AMN∽△DMA;
(2)证明:如图甲,过点C作CF∥AB交MN于点F,则△CFN∽△AMN,∴![]() .
.
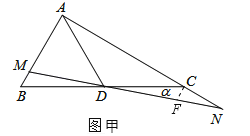
∵CF∥BM,∴∠B=∠DCF.在△CFD和△BMD中, 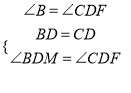 ,∴△CFD≌△BMD,∴BM=CF,∴
,∴△CFD≌△BMD,∴BM=CF,∴![]() ,∴
,∴![]() ,即
,即![]() ;
;
(3)猜想: ![]() +
+![]() =
=![]() 成立.理由如下:
成立.理由如下:
①如图乙,过D作MN∥M'N'交AB于M,交AC的延长线于N,则![]() ,∴
,∴![]() ,即
,即![]() ,由(2)知
,由(2)知![]() ,∴
,∴![]() ;
;
②如图丙,当过点D作M1N1∥M'N'交AB的延长线于M1,交AC1于N1,则同理可得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C、D四个车站的位置如图所示,A、B两站之间的距离AB=a﹣b,B、C两站之间的距离BC=2a﹣b,B、D两站之间的距离BD=
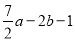 .
.(1)求A、C两站之间的距离AC.
(2)若A、C两站之间的距离AC=90km,求C、D两站之间的距离CD.
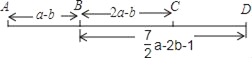
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,纸上有五个边长为1的小正方形组成的图形纸(图1),我们可以把它剪开拼成一个正方形(图2).

(1)图2中拼成的正方形的面积是 _________ ;边长是 _________ ;(填实数)
(2)请你在图3中画一个面积为5的正方形,要求所画正方形的顶点都在格点上.请用虚线画出.
(3)你能把十个小正方形组成的图形纸(图4),剪开并拼成正方形吗?若能,请仿照图2的形式把它重新拼成一个正方形.并求出它的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.

(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD的边AD在y轴上,抛物线
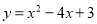 经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上。
经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上。(1)请直接写出下列各点的坐标:
A ,B ,C ,D ;
(2)若点P是抛物线上一动点(点P不与点A、点B重合),过点P作
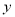 轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2。
轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2。①当线段PH=2GH时,求点P的坐标;
②当点P在直线BD下方时,点K在直线BD上,且满足△KPH∽△AEF,求△KPH面积的最大值。
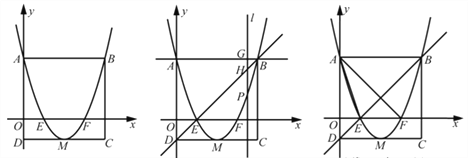
图1 图2 备用图
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,在平面直角坐标系中,点A,B,C都在坐标轴上,且OA=OB=OC,△ABC的面积为9,点P从C点出发沿y轴负方向以1个单位/秒的速度向下运动,连接PA,PB,D(﹣m,﹣m)为AC上的点(m>0)
(1)试分别求出A,B,C三点的坐标;
(2)设点P运动的时间为t秒,问:当t为何值时,DP与DB垂直且相等?请说明理由;
(3)如图2,若PA=AB,在第四象限内有一动点Q,连QA,QB,QP,且∠PQA=60°,当Q在第四象限内运动时,求∠APQ与∠PBQ的度数和.
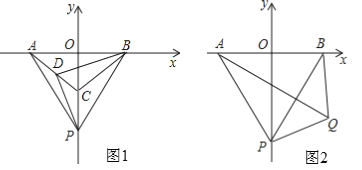
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是 ;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?

相关试题

