搜索
【题目】如图，在直角坐标系中，直线y=kx+4与x 轴正半轴交于一点A，与y轴交于点B，已知△OAB的面积为10，求这条直线的解析式。
参考答案：
【答案】
【解析】试题分析: 先根据坐标轴上点的坐标特征得到A（4k，0），B（0，4），再根据三角形面积公式得到
（
）4＝10，然后解方程求出k的值即可得到直线解析式．
试题解析:
当y＝0时，kx＋4＝0，解得x＝
，则A（
，0），
当x＝0时，y＝kx＋4＝4，则B（0，4），
因为△OAB的面积为10，
所以
（
）4＝10，解得k＝
，
所以直线解析式为y＝
x＋4．
点睛: 本题考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解析式时，先设y＝kx＋b；将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；解方程或方程组，求出待定系数的值，进而写出函数解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图
，某无人机于空中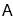
处探测到目标
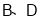的俯角分别是
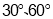,此时无人机的飞行高度
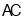为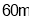
，随后无人机从
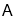处继续水平飞行
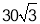m到达
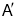处.(1)求
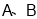之间的距离(2)求从无人机
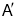上看目标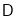
的俯角的正切值.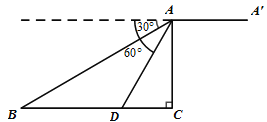
-
科目： 来源： 题型：
查看答案和解析>>【题目】某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如表：
原进价（元/张）
零售价（元/张）
成套售价（元/套）
餐桌
a
270
500元
餐椅
a﹣110
70
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同．
（1）求表中a的值；
（2）若该商场购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．该商场计划将一半的餐桌成套（一张餐桌和四张餐椅配成一套）销售，其余餐桌、餐椅以零售方式销售．请问怎样进货，才能获得最大利润？最大利润是多少？
（3）由于原材料价格上涨，每张餐桌和餐椅的进价都上涨了10元，按照（2）中获得最大利润的方案购进餐桌和餐椅，在调整成套销售量而不改变销售价格的情况下，实际全部售出后，所得利润比（2）中的最大利润少了2250元．请问本次成套的销售量为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一元二次方程x2+x﹣2=0，则方程的两根为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若三条直线交于一点，则共有对顶角(平角除外) （ ）
A．6对B．5对C．4对D．3对
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中,已知ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则点D的坐标是( )
A.(-2,1)
B.(-2,-1)
C.(-1,-2)
D.(-1,2) -
科目： 来源： 题型：
查看答案和解析>>【题目】清朝康熙皇帝是我国历史上对数学很有兴趣的帝王近日，西安发现了他的数学专著，其中有一文《积求勾股法》，它对“三边长为3、4、5的整数倍的直角三角形，已知面积求边长”这一问题提出了解法：“若所设者为积数（面积），以积率六除之，平方开之得数，再以勾股弦各率乘之，即得勾股弦之数”.用现在的数学语言表述是：“若直角三角形的三边长分别为3、4、5的整数倍，设其面积为S，则第一步：
＝m；第二步： 
＝k；第三步：分别用3、4、5乘以k，得三边长”.（1）当面积S等于150时，请用康熙的“积求勾股法”求出这个直角三角形的三边长；
（2）你能证明“积求勾股法”的正确性吗？请写出证明过程.
相关试题
