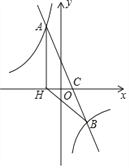
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数![]() 的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=
的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=![]() ,tan∠ACH=2,且点B的坐标为(4,n).
,tan∠ACH=2,且点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)8
;(2)8
【解析】(1)先求得AH、CH的长,再根据点O是CH中点确定出OH、CH的长,从而确定出点A的坐标,继而得到反比例函数的解析式,从而得到点B的坐标,利用待定系数法即可求得一次函数的解析式;
(2)根据三角形的面积公式进行求解即可得.
试题解析:(1)∵∠AHC=90°,tan∠ACH=2,∴![]() =2,
=2,
∵AC=4![]() ,AC2=AH2+CH2,∴CH=4,AH=8,
,AC2=AH2+CH2,∴CH=4,AH=8,
∵O为CH的中点,∴OH=CH=2,
∴A(-2,8),
把A(-2,8)代入y=![]() 中,得k=-16,
中,得k=-16,
所以反比例函数解析式为:![]() ,
,
把点B(4,n)代入![]() ,得:n=-4,所以B(4,-4),
,得:n=-4,所以B(4,-4),
把A(-2,8)、B(4,-4)分别代入y=ax+b,得
![]() ,解得:
,解得:![]() ,
,
所以一次函数解析式为:y=-2x+4;
(2)由题意可得S△BCH=![]() =8.
=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,平行四边形ABCD的周长是26cm,对角线AC与BD相交于点O, AC⊥AB,E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE =_____cm.

-
科目: 来源: 题型:
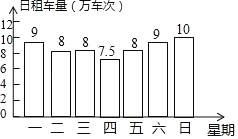
查看答案和解析>>【题目】摩拜公司为了调查在某市投放的共享单车使用情况,对4月份第一个星期中每天摩拜单车使用情况进行统计,结果如图所示.
(1)求这一个星期每天单车使用情况的众数、中位数和平均数;
(2)用(1)中的结果估计4月份一共有多少万车次?
(3)摩拜公司在该市共享单车项目中共投入9600万元,估计本年度共租车3200万车次,若每车次平均收入租车费0.75元,请估计本年度全年租车费收入占总投入的百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承中华优秀的传统文化,市教育局决定开展“经典诵读进校园”活动,某校园团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表:
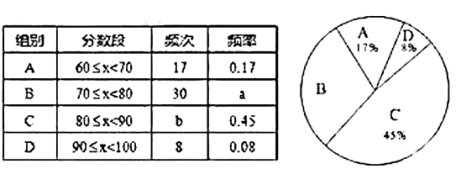
请根据所给信息,解答以下问题:
(1)表中
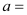 ;
;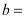 ;
;(2)请计算扇形统计图中
 组对应的圆心角的度数;
组对应的圆心角的度数;(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列举法或树状图法求甲、乙两名同学都被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】江津区某玩具商城在“六一”儿童节来临之际,以49元/个的价格购进某种玩具进行销售,并预计当售价为50元/个时,每天能售出50个玩具,且在一定范围内,当每个玩具的售价平均每提高0.5元时,每天就会少售出3个玩具。
(1)若玩具售价不超过60元/个,每天售出玩具总成本不高于686元,预计每个玩具售价的取值范围;
(2)在实际销售中,玩具城以(1)中每个玩具的最低售价及相应的销量为基础,进一步调整了销售方案,将每个玩具的售价提高了
 %,从而每天的销售量降低了
%,从而每天的销售量降低了 %,当每天的销售利润为147元时,求a的值.
%,当每天的销售利润为147元时,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:
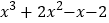 因式分解的结果为
因式分解的结果为 ,当
,当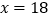 时,
时,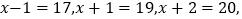 此时可以得到数字密码171920.
此时可以得到数字密码171920.(1)根据上述方法,当
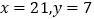 时,对于多项式
时,对于多项式 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式
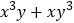 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);(3)若多项式
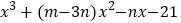 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当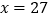 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
相关试题

