【题目】如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:
(1)旋转△ADF可得到哪个三角形?
(2)旋转中心是哪一点?旋转了多少度?
(3)BE与DF的数量关系、位置关系如何?为什么?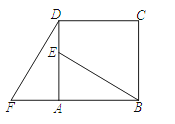
参考答案:
【答案】解:(1)旋转△ADF可得△ABE,
理由如下:
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠DAF=90°,
在△ADF和△ABE中, ,
,
∴△ADF≌△ABE,
∴旋转△ADF可得△ABE;
(2)由旋转的定义可知:旋转中心为A,因为AD=AB,所以AD和AB之间的夹角为旋转角即90°;
(3)BE=DF且BE⊥BE.理由如下:
延长BE交F于H点,如图,
∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90°,
∵△ABE按逆时针方向旋转90°△ADF,
∴BE=DF,∠1=∠2,
∵∠3=∠4,
∴∠DHB=∠BAE=90°,
∴BE⊥DF.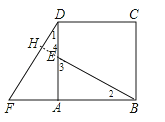
【解析】(1)旋转△ADF可得△ABE,通过证明△ADF≌△ABE即可说明问题;
(2)旋转的定义和旋转角的定义解答即可;
(3)根据旋转的性质得BE=DF,∠1=∠2,再根据三角形内角定理得到∠DHB=∠BAE=90°,所以BE⊥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个平面直角坐标系,已知点A,B,C,D的坐标分别为(﹣2,﹣3),(2,﹣2),(3,1),(﹣4,5)按要求完成下列各小题.

(1)请你在图中描出上述的四个点,并依次连接AB,BC,CD,DA,组成四边形ABCD;
(2)在(1)的基础上,将四边形ABCD先向下平移2个单位长度,再向右平移3个单位长度,得到四边形A′B′C′D′,请在图中画出四边形A′B′C′D′. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市“五一”共接待游客约3020000人次,“3020000”用科学记数法可表示为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E、F为对角线AC上的点,且AE=CF,试探索四边形DEBF的形状并说明你的理由.
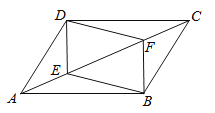
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:
[(a+b)(b﹣2a)﹣(a﹣2b)2+3b2]÷(﹣3a),其中a=﹣3,b=﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x+2)2+3的顶点坐标是( )
A.(﹣2,3)
B.(2,3)
C.(﹣2,﹣3)
D.(2,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
58
96
116
295
484
601
摸到白球的频率

0.58
0.64
0.58
0.59
0.605
0.601
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是
(3)试估算口袋中黑、白两种颜色的球有 只.
相关试题

