【题目】根据下列语句画图:
(1)画∠AOB=120°;
(2)画∠AOB的角平分线OC;
(3)反向延长OC得射线OD;
(4)分别在射线OA、OB、OD上画线段OE=OF=OG=2cm;
(5)连接EF、EG、FG;
(6)你能发现EF、EG、FG有什么关系?∠EFG、∠EGF、∠GEF有什么关系?
参考答案:
【答案】(1)图形见解析;(2)图形见解析;(3)图形见解析;(4)图形见解析;(5)图形见解析;(6)EF=EG=FG;∠EFG=∠EGF=∠FEG=60°.
【解析】
(1)(2)(3)(4)(5)见解析;
(6) 首先根据题意画出图形,然后再利用角平分线定理可直接证出
![]()
解:(1)(2)(3)(4)(5)如图所示:
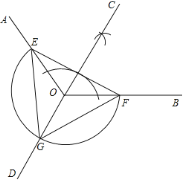
(6)![]()
理由:
![]()
![]() 三点在同一个圆上,
三点在同一个圆上,
![]()
![]()
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
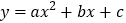 (a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
(a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:①16a﹣4b+c<0;②若P(﹣5,y1),Q(
 ,y2)是函数图象上的两点,则y1>y2;③a=﹣
,y2)是函数图象上的两点,则y1>y2;③a=﹣ c;④若△ABC是等腰三角形,则b=﹣
c;④若△ABC是等腰三角形,则b=﹣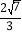 .其中正确的有______(请将结论正确的序号全部填上)
.其中正确的有______(请将结论正确的序号全部填上) -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学将组织七年级学生春游一天,由王老师和甲、乙两同学到客车租赁公司洽谈租车事宜.
(1)两同学向公司经理了解租车的价格,公司经理对他们说:“公司有45座和60座两种型号的客车可供租用,60座的客车每辆每天的租金比45座的贵100元.”王老师说:“我们学校八年级昨天在这个公司租了5辆45座和2辆60座的客车,一天的租金为1600元,你们能知道45座和60座的客车每辆每天的租金各是多少元吗”甲、乙两同学想了一下,都说知道了价格.
聪明的你知道45座和60座的客车每辆每天的租金各是多少元吗?
(2)公司经理问:“你们准备怎样租车”,甲同学说:“我的方案是只租用45座的客车,可是会有一辆客车空出30个座位”;乙同学说“我的方案只租用60座客车,正好坐满且比甲同学的方案少用两辆客车”,王老师在﹣旁听了他们的谈话说:“从经济角度考虑,还有别的方案吗”?如果是你,你该如何设计租车方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F.
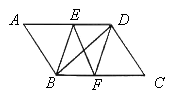
【1】△ABE≌△CDF
【2】若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知线段
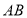 ,点
,点 的坐标为
的坐标为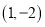 ,点
,点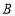 的坐标为
的坐标为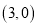 ,如图1所示.
,如图1所示.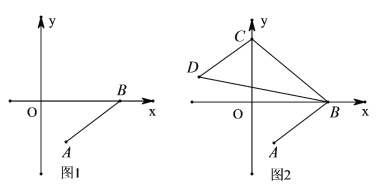
(1)平移线段

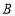 到线段
到线段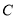
 ,使点
,使点 的对应点为,点
的对应点为,点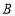 的对应点为
的对应点为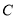 ,若点
,若点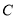 的坐标为
的坐标为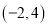 ,求点
,求点 的坐标;
的坐标; (2)平移线段

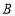 到线段
到线段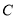
 ,使点
,使点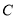 在
在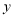 轴的正半轴上,点
轴的正半轴上,点 在第二象限内(
在第二象限内( 与
与 对应,
对应, 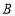 与
与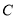 对应),连接
对应),连接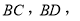 如图2所示.若
如图2所示.若 表示△BCD的面积),求点
表示△BCD的面积),求点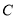 、
、 的坐标;
的坐标; (3)在(2)的条件下,在
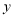 轴上是否存在一点
轴上是否存在一点 ,使
,使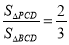 ?若存在,求出点
?若存在,求出点 的坐标,
的坐标, -
科目: 来源: 题型:
查看答案和解析>>【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数
频数
频率
0≤x<4000
8
a
4000≤x<8000
15
0.3
8000≤x<12000
12
b
12000≤x<16000
c
0.2
16000≤x<20000
3
0.06
20000≤x<24000
d
0.04
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明将一个正方形纸剪去一个宽为
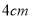 的长条后, 再从剩下的长方形纸片上剪去一个宽为
的长条后, 再从剩下的长方形纸片上剪去一个宽为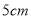 的长条,如果两次剪下的长条面积正好相等,那么剩下的白色长方形纸的面积为( )
的长条,如果两次剪下的长条面积正好相等,那么剩下的白色长方形纸的面积为( )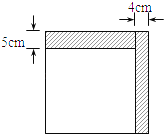
A.
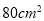 B.
B.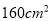 C.
C.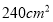 D.
D.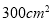
相关试题

