【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.

参考答案:
【答案】(1)a=0.16,b=0.24,c=10,d=2,图见解析;(2)11340名;(3)![]() .
.
【解析】试题分析:(1)根据频率=频数÷总数可得答案;
(2)用样本中超过12000步(包含12000步)的频率之和乘以总人数可得答案;
(3)画树状图列出所有等可能结果,根据概率公式求解可得.
试题解析:解:(1)a=8÷50=0.16,b=12÷50=0.24,c=50×0.2=10,d=50×0.04=2,补全频数分布直方图如下:
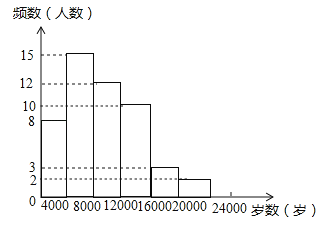
(2)37800×(0.2+0.06+0.04)=11340.
答:估计日行走步数超过12000步(包含12000步)的教师有11340名;
(3)设16000≤x<20000的3名教师分别为A、B、C,20000≤x<24000的2名教师分别为X、Y,画树状图如下:
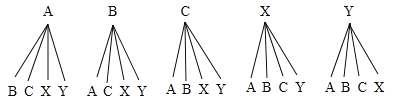
由树状图可知,被选取的两名教师恰好都在20000步(包含20000步)以上的概率为![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F.
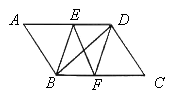
【1】△ABE≌△CDF
【2】若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列语句画图:
(1)画∠AOB=120°;
(2)画∠AOB的角平分线OC;
(3)反向延长OC得射线OD;
(4)分别在射线OA、OB、OD上画线段OE=OF=OG=2cm;
(5)连接EF、EG、FG;
(6)你能发现EF、EG、FG有什么关系?∠EFG、∠EGF、∠GEF有什么关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知线段
 ,点
,点 的坐标为
的坐标为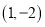 ,点
,点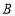 的坐标为
的坐标为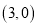 ,如图1所示.
,如图1所示.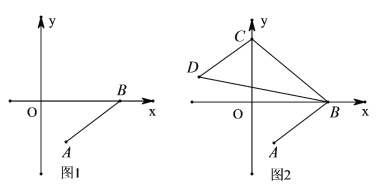
(1)平移线段

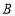 到线段
到线段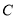
 ,使点
,使点 的对应点为,点
的对应点为,点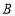 的对应点为
的对应点为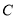 ,若点
,若点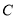 的坐标为
的坐标为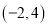 ,求点
,求点 的坐标;
的坐标; (2)平移线段

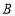 到线段
到线段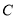
 ,使点
,使点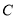 在
在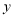 轴的正半轴上,点
轴的正半轴上,点 在第二象限内(
在第二象限内( 与
与 对应,
对应, 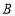 与
与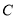 对应),连接
对应),连接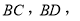 如图2所示.若
如图2所示.若 表示△BCD的面积),求点
表示△BCD的面积),求点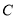 、
、 的坐标;
的坐标; (3)在(2)的条件下,在
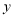 轴上是否存在一点
轴上是否存在一点 ,使
,使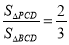 ?若存在,求出点
?若存在,求出点 的坐标,
的坐标, -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明将一个正方形纸剪去一个宽为
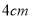 的长条后, 再从剩下的长方形纸片上剪去一个宽为
的长条后, 再从剩下的长方形纸片上剪去一个宽为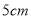 的长条,如果两次剪下的长条面积正好相等,那么剩下的白色长方形纸的面积为( )
的长条,如果两次剪下的长条面积正好相等,那么剩下的白色长方形纸的面积为( )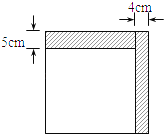
A.
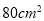 B.
B.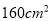 C.
C.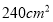 D.
D.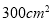
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=AC.D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①△AED≌△AEF;
②△ABE∽△ACD;
③BE+DC=DE;
④BE2+DC2=DE2.
其中正确的是( )

A.②④ B.①④ C.②③ D.①③
-
科目: 来源: 题型:
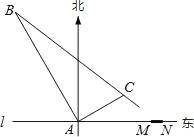
查看答案和解析>>【题目】在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距
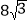 km的C处.
km的C处.(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
相关试题

