【题目】如图,以△ABC的一边AB为直径作⊙O, ⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E.
(1) 求证:DE⊥AC;
(2) 连结OC交DE于点F,若![]() ,求
,求![]() 的值.
的值.

参考答案:
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)连接OD,根据三角形的中位线定理可求出OD∥AC,根据切线的性质可证明DE⊥OD,进而得证.
(2)过O作OF⊥BD,根据等腰三角形的性质及三角函数的定义用OB表示出OF、CF的长,根据三角函数的定义求解.
试题解析:(1)连接OD . ∵DE是⊙O的切线,
∴DE⊥OD,即∠ODE=90° .
∵AB是⊙O的直径,
∴O是AB的中点.
又∵D是BC的中点, .
∴OD∥AC .
∴∠DEC=∠ODE= 90° .
∴DE⊥AC .
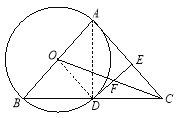
(2)连接AD . ∵OD∥AC,
∴![]() .
.
∵AB为⊙O的直径, ∴∠ADB= ∠ADC =90° .
又∵D为BC的中点,
∴AB=AC.
∵sin∠ABC= ![]() =
=![]() , 故设AD= 3x , 则AB=AC=4x , OD= 2x .
, 故设AD= 3x , 则AB=AC=4x , OD= 2x .
∵DE⊥AC, ∴∠ADC= ∠AED= 90°.
∵∠DAC= ∠EAD, ∴△ADC∽△AED.
∴![]() .
.
∴![]() .
.
∴![]() . ∴
. ∴![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2﹣6x+5用配方法化成y=(x﹣h)2+k的形式,下列结果中正确的是( )
A.y=(x﹣6)2+5
B.y=(x﹣3)2+5
C.y=(x﹣3)2﹣4
D.y=(x+3)2﹣9 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价;
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若y=xm﹣2是二次函数,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣3,y1),B(2,y2)在抛物线y=x2﹣5x上,则y1y2 . (填“>”,“<”或“=”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年“五·一”节期间,某商场举行抽奖促销活动.抽奖办法是:在一个不透明的袋子中装有四个标号分别为1,2,3,4的小球,它们的形状、大小、质地等完全相同.抽奖者第一次摸出一个小球,不放回,第二次再摸出一个小球,若两次摸出的小球中有一个小球标号为“1”,则获奖.
(1)请你用树形图或列表法表示出抽奖所有可能出现的结果;
(2)求抽奖人员获奖的概率.
-
科目: 来源: 题型:
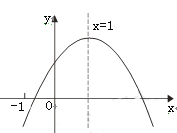
查看答案和解析>>【题目】已知二次函数
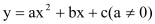 的图象如图所示,有下列5个结论:
的图象如图所示,有下列5个结论:①
 ; ②
; ②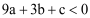 ; ③
; ③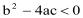 ; ④
; ④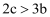 ;⑤
;⑤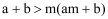 (
(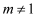 的实数). 其中正确的结论有( )
的实数). 其中正确的结论有( )A.2个 B.3个 C.4个 D.5个
相关试题

