Question

【题目】某商店欲购进甲、乙两种商品，已知甲的进价是乙的进价的一半，进3件甲商品和1件乙商品恰好用200元．甲、乙两种商品的售价每件分别为80元、130元，该商店决定用不少于6710元且不超过6810元购进这两种商品共100件．

（1）求这两种商品的进价；

（2）该商店有几种进货方案？哪种进货方案可获得最大利润，最大利润是多少？

Answer 1

【答案】（1）甲商品的进价为40元，乙商品的进价为80元；（2）该商店有3种进货方案；当甲种商品进货30件，乙商品进货70件时可获得最大利润，最大利润为4700元

【解析】

试题分析：（1）设甲商品的进价为x元，乙商品的进价为y元，就有x=y，3x+y=200，由这两个方程构成方程组求出其解即可以；

（2）设购进甲种商品m件，则购进乙种商品（100﹣m）件，根据不少于6710元且不超过6810元购进这两种商品100件建立不等式，求出其值就可以得出进货方案，设利润为W元，根据利润=售价﹣进价建立解析式就可以求出结论．

解：设甲商品的进价为x元，乙商品的进价为y元，由题意，得：

，

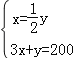解得：．

答：甲商品的进价为40元，乙商品的进价为80元；

（2）设购进甲种商品m件，则购进乙种商品（100﹣m）件，由题意，得：

，

解得：29≤m≤32

∵m为整数，

∴m=30，31，32，

故有三种进货方案：

方案1，甲种商品30件，乙商品70件，

方案2，甲种商品31件，乙商品69件，

方案3，甲种商品32件，乙商品68件，

设利润为W元，由题意，得

W=40m+50（100﹣m），

=﹣10m+5000

∵k=﹣10＜0，

∴W随m的增大而减小，

∴m=30时，W最大=4700．

答：该商店有3种进货方案；当甲种商品进货30件，乙商品进货70件时可获得最大利润，最大利润为4700元．