【题目】为了了解某学校初四年级学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):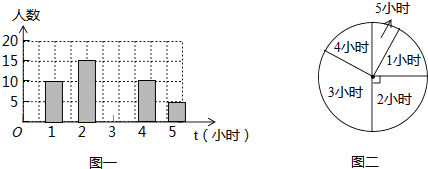
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
参考答案:
【答案】
(1)
解:①∵课外阅读时间为2小时的所在扇形的圆心角的度数为90°,
∴其所占的百分比为 ![]() =
= ![]() ,
,
∵课外阅读时间为2小时的有15人,
∴m=15÷ ![]() =60;
=60;
②依题意得: ![]() ×360°=30°;
×360°=30°;
③第三小组的频数为:60﹣10﹣15﹣10﹣5=20,
补全条形统计图为:

(2)
解:∵课外阅读时间为3小时的20人,最多,
∴众数为 3小时;
∵共60人,中位数应该是第30和第31人的平均数,且第30和第31人阅读时间均为3小时,
∴中位数为3小时;
平均数为: ![]() =2.75小时
=2.75小时
【解析】(1)①根据2小时所占扇形的圆心角的度数确定其所占的百分比,然后根据条形统计图中2小时的人数求得m的值;②结合周角是360度进行计算;③求得总人数后减去其他小组的人数即可求得第三小组的人数;(2)利用众数、中位数的定义及平均数的计算公式确定即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=﹣x2+6x上一点,且在x轴上方,则△BCD面积的最大值为 .
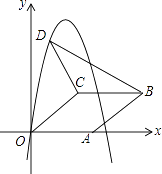
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
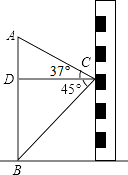
-
科目: 来源: 题型:
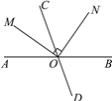
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.
(1)若∠BOD=70°,求∠AOM和∠CON的度数;
(2)若∠BON=50°,求∠AOM和∠CON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P1、P2是反比例函数y=
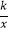 (k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点. 
(1)求反比例函数的解析式.
(2)①求P2的坐标. ②根据图象直接写出在第一象限内当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y=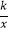 的函数值.
的函数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于点E,BE的延长线交CD于点F,且∠1+∠2=90°.猜想∠2与∠3的关系并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax+bx+c的图像如图所示,则代数式(a+b)-c的值( ).
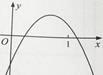
A.大于0
B.等于0
C.小于0
D.不确定
相关试题

