【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)试求∠DAE的度数;
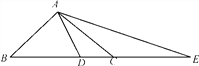
(2)如果把原题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?为什么?
参考答案:
【答案】(1) 45°(2)不变
【解析】试题分析:(1)根据等腰直角三角形的性质求出∠B=∠ACB=45°,根据等边对等角的性质求出∠BAD=∠BDA,∠E=∠CAE,再根据三角形的一个外角等于和它不相邻的两个内角的和即可求出∠DAE的度数;
(2)由BD=BA可得∠BAD=∠BDA=![]() (180°-∠B),由CE=CA可得∠E=∠CAE=
(180°-∠B),由CE=CA可得∠E=∠CAE=![]() ∠ACB=
∠ACB=![]() (90°-∠B),再根据三角形外角的性质即可得到结论。
(90°-∠B),再根据三角形外角的性质即可得到结论。
(1)∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∵CE=CA,
∴∠E=∠CAE=![]() ×45°=22.5°,
×45°=22.5°,
∴∠DAE=∠BDA-∠E=67.5°-22.5°=45°;
(2)∵BD=BA,
∴∠BAD=∠BDA=![]() (180°-∠B),
(180°-∠B),
∵CE=CA,
∴∠E=∠CAE=![]() ∠ACB=
∠ACB=![]() (90°-∠B),
(90°-∠B),
∴∠DAE=∠BDA-∠E=![]() (180°-∠B)-
(180°-∠B)-![]() (90°-∠B)=90°-
(90°-∠B)=90°-![]() ∠B-45°+
∠B-45°+![]() ∠B=45°,
∠B=45°,
即∠DAE的度数不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下表: 我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
序号
1
2
3
…
图形
x x
y
x xx x x
y y
x x x
y y
x x xx x x x
y y y
x x x x
y y y
x x x x
y y y
x x x x…
(1)第3格的“特征多项式”为 , 第4格的“特征多项式”为 , 第n格的“特征多项式”为;
(2)若第1格的“特征多项式”的值为﹣10,第2格的“特征多项式”的值为﹣16. ①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下图中我国四大银行的商标图案中既是轴对称图形又是中心对称图形的个数有( )
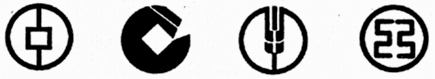
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(﹣ )2=﹣
)2=﹣ 
B.(3a2)3=9a6
C.5﹣3÷5﹣5=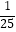
D.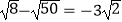
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列三行数,并完成后面的问题:
①﹣2,4,﹣8,16,﹣32,…;
②l,﹣2,4,﹣8,16,…;
③0,﹣3,3,﹣9,15,…
(1)思考第①行数的规律,写出第n个数字是多少(用含n的式子表示);
(2)第②行数和第①行数有什么关系?第③行数和第②行数又有什么关系?
(3)设x,y,z分别表示第①②③行数的第10个数字,求x+y+z的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,边AB的垂直平分线MN交AC于点D,若△BCD的周长为24cm,BC=10cm,则AB的长为cm.

相关试题

