【题目】某农场急需氨肥8 t,在该农场南北方向分别有A,B两家化肥公司,A公司有氨肥3 t,每吨售价750元;B公司有氨肥7 t,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输质量a(单位:t)的关系如图所示.
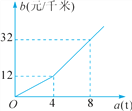
(1)根据图象求出b关于a的函数表达式(写出自变量的取值范围).
(2)若农场到B公司的路程是农场到A公司路程的2倍,农场到A公司的路程为m(km),设农场从A公司购买x(t)氨肥,购买8 t氨肥的总费用为y元(总费用=购买铵肥的费用+运输费用),求出y关于x的函数表达式(m为常数),并向农场建议总费用最低的购买方案.
参考答案:
【答案】(1)b=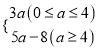 ;(2)当m>
;(2)当m>![]() 时,到A公司买3 t,到B公司买5 t费用最低;当m=
时,到A公司买3 t,到B公司买5 t费用最低;当m=![]() 时,到A公司或B公司买费用一样;当m<
时,到A公司或B公司买费用一样;当m<![]() 时,到A公司买1 t,到B公司买7 t,费用最低.
时,到A公司买1 t,到B公司买7 t,费用最低.
【解析】试题分析:(1)利用待定系数法分别求出当0≤a≤4和当a>4时,b关于a的函数解析式;
(2)由于1≤x≤3,则到A公司的运输费用满足b=3a,到B公司的运输费用满足b=5a﹣8,利用总费用=购买铵肥费用+运输费用得到y=750x+3mx+(8﹣x)×700+[5(8﹣x)﹣8]2m,然后进行整理,再利用一次函数的性质确定费用最低的购买方案.
试题解析:(1)当0≤a≤4时,设b=ka,把(4,12)代入得4k=12,解得k=3,所以b=3a;
当a>4,设![]() ,把(4,12),(8,32)代入得:
,把(4,12),(8,32)代入得: ![]() ,解得:
,解得: ![]() ,所以
,所以![]() ;
;
∴![]() ;
;
(2)∵1≤x≤3,∴y=750x+3mx+(8﹣x)×700+[5(8﹣x)﹣8]2m,∴![]() ,当m>
,当m>![]() 时,到A公司买3吨,到B公司买5吨,费用最低;当m<
时,到A公司买3吨,到B公司买5吨,费用最低;当m<![]() 时,到A公司买1吨,到B公司买7吨,费用最低.
时,到A公司买1吨,到B公司买7吨,费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】每支晨光自动笔的价格是2元,请你根据所给条件完成下表:
x(支)
1
2
3
4
5
6
…
y(元)
2
…
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列图形:①等边三角形,②平行四边形,③菱形,④矩形,其中既是轴对称图形又是中心对称图形的有( ).
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平直角坐标系中,如果抛物线y=4x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( )
A.y=4(x﹣2)2+2B.y=4(x+2)2﹣2
C.y=4(x﹣2)2﹣2D.y=4(x+2)2+2
-
科目: 来源: 题型:
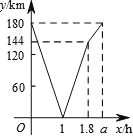
查看答案和解析>>【题目】甲、乙两车分别从A、B两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到B地停止,乙车行驶到A地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为y(km),乙车行驶的时间为x(h),y与x之间的函数图象如图所示.
(1)求甲车行驶的速度.
(2)求甲车到达B地后y与x之间的函数关系式.
(3)当两车相遇后,两车之间的路程是160km时,求乙车行驶的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“五一”劳动节,某中学组织了甲、乙两个义务劳动小组,甲组x人,乙组y人,到“中华路”和“青年路”打扫卫生,根据打扫卫生的进度,学校随时调整两组人数,如果从甲组调50人去乙组,则乙组人数为甲组人数的2倍;如果从乙组调m人去甲组,则甲组人数为乙组人数的3倍.
(1)求出x与m之间的函数表达式.
(2)问:当m为何值时,甲组人数最少,最少是多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=
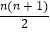 .
.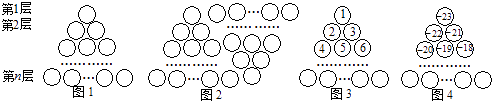
如果图中的圆圈共有11层,请问:自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层中间这个圆圈中的数是;自上往下,在每个圆圈中按图4的方式填上一串连续的整数
﹣23,﹣22,﹣21,﹣20,…,则所有圆圈中各数之和为 .
相关试题

