【题目】初步探究
如图①,过点P的两条直线分别与⊙O相切于点A,与⊙O相交于B、C两点,且AC恰好经过圆心O.求证△PAB∽△PCA.
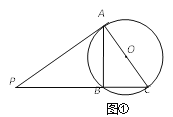
进一步探究
如图②若其他条件不变,但AC不经过圆心O.上述结论是否成立?请说明理由.

尝试应用
如图③,PA=3,PB=![]() ,⊙O的半径为2,请直接写出直线PC上一点与圆心O的最短距离.
,⊙O的半径为2,请直接写出直线PC上一点与圆心O的最短距离.

参考答案:
【答案】(1)证明见解析;(2)成立.理由见解析(3)1.
【解析】试题分析:(1)、根据切线的性质得出∠PAB+∠BAC=90°,根据直径的性质得出∠BAC+∠C=90°,从而得出∠PAB=∠C,结合公共角得出三角形相似;(2)、连接AO,延长AO交⊙O于D,连接BD,然后根据第一题相似的方法得出三角形相似;(3)、当AC为直径时以及三角形相似得出最短距离.
试题解析:(1)∵PA与⊙O相切, ∴∠PAC=90° ∴∠1+∠PAB=90°.
∵AC是⊙O的直径 ∴∠1+∠C=90° ∴∠PAB=∠C 又∵∠P=∠P ∴△PAB∽△PCA
(2)成立.连接AO,延长AO交⊙O于D,连接BD.
∵PA与⊙O相切 ∴∠PAD=90° ∴∠1+∠PAB=90° ∵AD是⊙O的直径
∴∠1+∠D=90° ∴∠PAB=∠D 又∵∠C=∠D ∴∠PAB=∠C
又∵∠P=∠P ∴△PAB∽△PCA.
(3)1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年6月18日为父亲节,某校准备开展形式多样的感恩教育活动.下面图①、图②分别是该校调查部分学生是否知道父亲生日情况的扇形统计图和频数分布直方图.
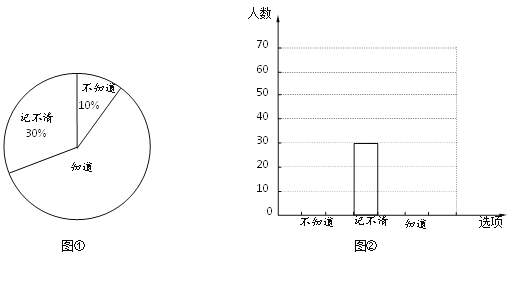
根据上图信息,解答下列问题:
(1)本次被调查的学生总数有 人,并补全频数分布直方图②;
(2)在扇形统计图中,学生知道父亲生日的区域圆心角为 o;
(3)若这所学校共有学生1500人,请你估计该校知道父亲生日的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠B=90°,AB=BD,AD=CD,求∠CAD的度数.
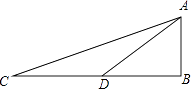
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级有15名同学参加校运会百米比赛,预赛成绩各不相同,前7名才有资格参加决赛,小明已经知道了自己的成绩,但他想知道自己能否进入决赛,还需要知道这15名同学成绩的_____.(填“极差”、“众数”或“中位数”)
-
科目: 来源: 题型:
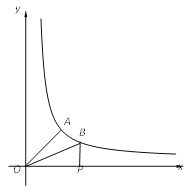
查看答案和解析>>【题目】如图,已知A、B是反比例函数y=
 图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4, tan∠BOP=
图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4, tan∠BOP= .
.(1)求点A的坐标;
(2)连接AB,求四边形AOPB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据共有50个,分成5组后其中前四组的频数分别是3、17、15、5, 则第5组数据的频率为________.
相关试题

