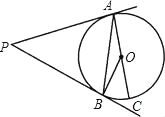
【题目】已知:如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,∠BAC=35°,求∠P的度数.
参考答案:
【答案】70°.
【解析】
试题分析:由PA与PB都为圆的切线,根据切线的性质得到OA与AP垂直,OB与BP垂直,可得出∠OAP与∠OBP都为直角,又OA=OB,根据等边对等角可得∠ABO与∠BAC相等,由∠BAC的度数求出∠ABO的度数,进而利用三角形的内角和定理求出∠AOB的度数,在四边形APBO中,利用四边形的内角和定理即可求出∠P的度数.
试题解析:∵PA,PB分别是⊙O的切线,
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°,
∵OA=OB,∠BAC=35°
∴∠ABO=∠BAC=35°,
∴∠AOB=180°-35°-35°=110°,
在四边形APBO中,∠OAP=∠OBP=90°,∠AOB=110°,
则∠P=360°-(∠OAP+∠OBP+∠AOB)=70°.
-
科目: 来源: 题型:
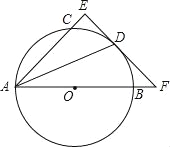
查看答案和解析>>【题目】如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
求证:EF与圆O相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形有两条边长为4和9,则该三角形的周长是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点M(1,2)关于x轴对称的点的坐标为( )
A (-1,-2) B (-1,2) C (1,-2) D (2,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元.(注:毛利润=售价﹣进价)
-
科目: 来源: 题型:
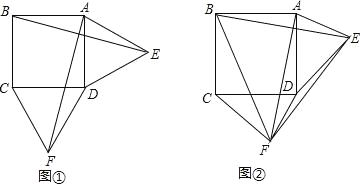
查看答案和解析>>【题目】问题背景:在正方形ABCD的外侧,作△ADE和△DCF,连结AF、BE.
特例探究:如图①,若△ADE与△DCF均为等边三角形,试判断线段AF与BE的数量关系和位置关系,并说明理由;
拓展应用:如图②,在△ADE与△DCF中,AE=DF,ED=FC,且BE=4,则四边形ABFE的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,线段AB=7,BC=3,则AC长为_____.
相关试题

