搜索
【题目】夏季是垂钓的好季节．一天甲、乙两人到松花江的
处钓鱼，突然发现在
处有一人不慎落入江中呼喊救命．如图，在处测得处在的北偏东
方向，紧急关头，甲、乙二人准备马上救人，只见甲马上从处跳水游向处救人；此时乙从沿岸边往正东方向奔跑40米到达
处，再从处下水游向处救人，已知处在的北偏东
方向上，且甲、乙二人在水中游进的速度均为1米/秒，乙在岸边上奔跑的速度为8米/秒．（注：水速忽略不计）
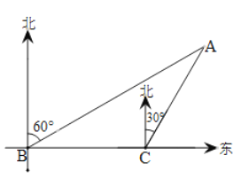
（1）求
、
的长．
（2）试问甲、乙二人谁能先救到人，请通过计算说明理由．（
）
参考答案：
【答案】（1）
米，
米，（2）乙先到达救人地点．
【解析】
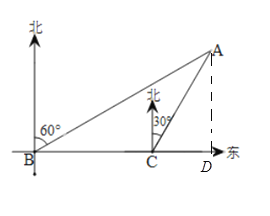
（1）过点A作AD⊥CD于点D，分别在Rt△ABD、Rt△ACD中用式子表示
再利用锐角三角函数列方程，解方程即可．
（2）分别计算出甲乙到达落水点的时间即可得到答案．
解（1）；过点A作AD⊥CD于点D，由题意得：
设
则
（2）
乙在水中所花时间为：
乙到达的时间为：
甲到达的时间为：
乙先到达救人地点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，为了测量某建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地面上向建筑物前进了100 m，此时自B处测得建筑物顶部的仰部角是45°．已知测角仪的高度是1．5 m，请你计算出该建筑物的高度．（取≈1．732，结果精确到1 m）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，用长为6m的铝合金条制成“日”字形窗框，若窗框的宽为xm，窗户的透光面积为ym2（铝合金条的宽度不计）．
（1）求出y与x的函数关系式；
（2）如何安排窗框的长和宽，才能使得窗户的透光面积最大？并求出此时的最大面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解下列分式方程：
（1）
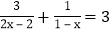； （2）
- 
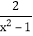=1 ； （3）
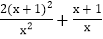-6 =0 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，方格纸中每个小正方形的边长为1cm，平移图中的△ABC，使点B移到点B1的位置．
（1）利用方格和直尺画图
①画出平移后的△A1B1C1
②画出AB边上的中线CD；
③画出BC边上的高AH；
（2）线段A1C1与线段AC的位置关系与数量关系为 ；
（3）△A1B1C1的面积为 cm2；△BCD的面积为 cm2．
-
科目： 来源： 题型：
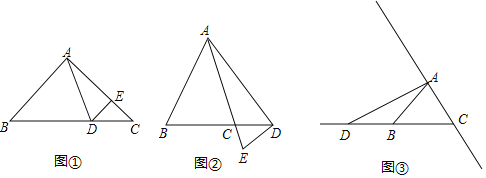
查看答案和解析>>【题目】如图①，在△ABC中，∠B＝∠C，点D在BC边上，点E在AC边上，且∠ADE＝∠AED，连结DE．
（1）若∠BAC＝100°，∠DAE＝40°，则∠CDE＝ ，此时
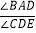＝ ；（2）若点D在BC边上（点B、C除外）运动，试探究∠BAD与∠CDE的数量关系并说明理由；
（3）若点D在线段BC的延长线上，点E在线段AC的延长线上（如图②），其余条件不变，请直接写出∠BAD与∠CDE的数量关系： ；
（4）若点D在线段CB的延长线上（如图③）、点E在直线AC上，∠BAD＝26°，其余条件不变，则∠CDE＝ °（友情提醒：可利用图③画图分析）
-
科目： 来源： 题型：
查看答案和解析>>【题目】图①为一种平板电脑保护套的支架效果图，AM固定于平板电脑背面，与可活动的MB、CB部分组成支架．平板电脑的下端N保持在保护套CB上．不考虑拐角处的弧度及平板电脑和保护套的厚度，绘制成图②．其中AN表示平板电脑，M为AN上的定点，AN＝CB＝20 cm，AM＝8 cm，MB＝MN．我们把∠ANB叫做倾斜角．
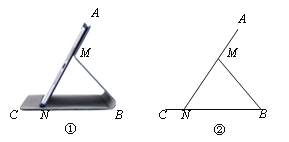
（1）当倾斜角为45°时，求CN的长；
（2）按设计要求，倾斜角能小于30°吗？请说明理由．
相关试题
