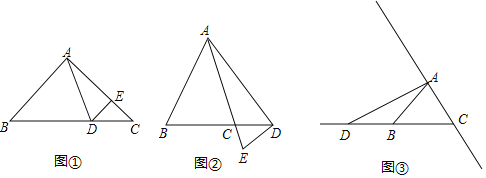
【题目】如图①,在△ABC中,∠B=∠C,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)若∠BAC=100°,∠DAE=40°,则∠CDE= ,此时![]() = ;
= ;
(2)若点D在BC边上(点B、C除外)运动,试探究∠BAD与∠CDE的数量关系并说明理由;
(3)若点D在线段BC的延长线上,点E在线段AC的延长线上(如图②),其余条件不变,请直接写出∠BAD与∠CDE的数量关系: ;
(4)若点D在线段CB的延长线上(如图③)、点E在直线AC上,∠BAD=26°,其余条件不变,则∠CDE= °(友情提醒:可利用图③画图分析)
参考答案:
【答案】(1)30°,2;(2)∠BAD=2∠CDE;理由见解析;(3)∠BAD=2∠CDE ;(4)∠CDE=13或77°
【解析】
(1)根据三角形内角和与三角形外角的性质可得结论;
(2)设∠DAE=x,∠BAC=y,同理可得∠BAD与∠CDE的数量关系;
(3)设∠DAE=x,∠BAC=y,同理可得∠BAD与∠CDE的数量关系;
(4)分两种情况讨论,同理可计算∠CDE的度数.
解:(1)如图,
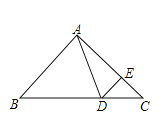
∵∠DAE=40°,∠ADE=∠AED,
∴∠ADE=70°,
∵∠BAC=100°,
∴∠BAD=∠BAC﹣∠DAE=100°﹣40°=60°,
∵∠B=∠C=40°,
∴∠ADC=∠B+∠BAD=40°+60°=100°,
∴∠CDE=30°,
∴![]() =2,
=2,
故答案为:30°,2;
(2)如图,∠BAD与∠CDE的数量关系是:∠BAD=2∠CDE;

理由是:设∠DAE=x,∠BAC=y,则∠BAD=y﹣x,
∵∠DAE=x,∠ADE=∠AED,
∴∠ADE=![]() ,
,
∵∠B=∠C=![]() ,
,
∴∠ADC=∠B+∠BAD=![]() +y﹣x=90°+
+y﹣x=90°+![]() y﹣x,
y﹣x,
∴∠CDE=∠ADC﹣∠ADE=90°+![]() y﹣x﹣
y﹣x﹣![]() =
=![]() ,
,
∴∠BAD=2∠CDE;
(3)如图,∠BAD与∠CDE的数量关系:∠BAD=2∠CDE,
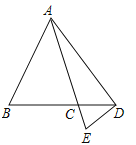
理由是:设∠DAE=x,∠BAC=y,则∠BAD=x+y,
∵∠DAE=x,∠ADE=∠AED,
∴∠ADE=∠E=![]() ,
,
∵∠B=![]() ,
,
∴∠ACD=∠B+∠BAC=∠E+∠CDE,
∴![]() +y=
+y=![]() +∠CDE,
+∠CDE,
∴∠CDE=![]() (x+y),
(x+y),
∴∠BAD=2∠CDE;
故答案为:∠BAD=2∠CDE;
(4)分两种情况:
①当E在射线CA上时,如图所示,
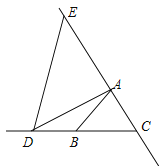
设∠DAE=x,∠BAC=y,则x+y=180°﹣26°=154°,
∵∠DAE=x,∠ADE=∠AED,
∴∠AED=![]() ,
,
∵∠C=![]() ,
,
△CDE中,∠CDE=180°﹣∠AED﹣∠C=180°﹣![]() ﹣
﹣![]() =
=![]() (x+y)=
(x+y)=![]() =77°
=77°
②当E在射线AC上时,如图所示,
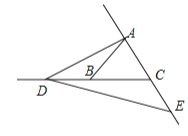
设∠DAE=x,∠BAC=y,则x﹣y=26°,
∵∠DAE=x,∠ADE=∠AED,
∴∠AED=![]() ,
,
∵∠ACB=![]() ,
,
△CDE中,∠CDE=∠ACB﹣∠AED=![]() ﹣
﹣![]() =
=![]() (x﹣y)=
(x﹣y)=![]() =13°,
=13°,
综上,∠CDE=13°或77°;
故答案为:13或77.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列分式方程:
(1)
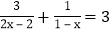 ;
; (2)
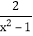 -
-  =1 ;
=1 ; (3)
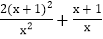 -6 =0
-6 =0 -
科目: 来源: 题型:
查看答案和解析>>【题目】夏季是垂钓的好季节.一天甲、乙两人到松花江的
 处钓鱼,突然发现在
处钓鱼,突然发现在 处有一人不慎落入江中呼喊救命.如图,在
处有一人不慎落入江中呼喊救命.如图,在 处测得
处测得 处在
处在 的北偏东
的北偏东 方向,紧急关头,甲、乙二人准备马上救人,只见甲马上从
方向,紧急关头,甲、乙二人准备马上救人,只见甲马上从 处跳水游向
处跳水游向 处救人;此时乙从
处救人;此时乙从 沿岸边往正东方向奔跑40米到达
沿岸边往正东方向奔跑40米到达 处,再从
处,再从 处下水游向
处下水游向 处救人,已知
处救人,已知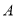 处在
处在 的北偏东
的北偏东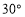 方向上,且甲、乙二人在水中游进的速度均为1米/秒,乙在岸边上奔跑的速度为8米/秒.(注:水速忽略不计)
方向上,且甲、乙二人在水中游进的速度均为1米/秒,乙在岸边上奔跑的速度为8米/秒.(注:水速忽略不计)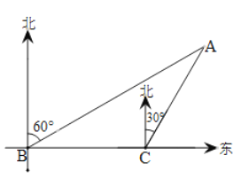
(1)求
 、
、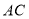 的长.
的长.(2)试问甲、乙二人谁能先救到人,请通过计算说明理由.(
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长为1cm,平移图中的△ABC,使点B移到点B1的位置.
(1)利用方格和直尺画图
①画出平移后的△A1B1C1
②画出AB边上的中线CD;
③画出BC边上的高AH;
(2)线段A1C1与线段AC的位置关系与数量关系为 ;
(3)△A1B1C1的面积为 cm2;△BCD的面积为 cm2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②.其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN.我们把∠ANB叫做倾斜角.
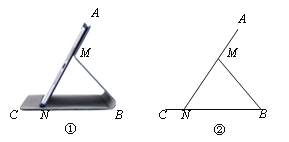
(1)当倾斜角为45°时,求CN的长;
(2)按设计要求,倾斜角能小于30°吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.

(1)求证:△BOE≌△DOF;
(2)若
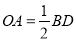 ,则四边形ABCD是什么特殊四边形?请说明理由.
,则四边形ABCD是什么特殊四边形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,延长平行四边形
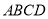 的边
的边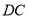 到点
到点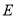 ,使
,使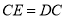 ,连接
,连接 交
交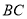 于点
于点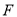 .
.(1)求证:
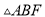 ≌
≌ .
.(2)连接
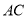 、
、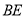 ,若
,若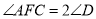 ,求证四边形
,求证四边形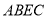 是矩形.
是矩形.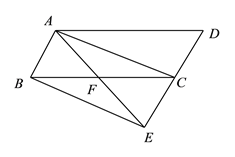
相关试题

