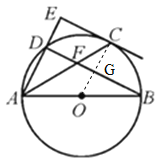
【题目】如图,AB为⊙O的直径,C、D两点均在⊙O上,过点C作CE⊥AD于点E,且AC平分∠BAD.
(1)求证:CE为⊙O的切线;
(2)连结BD交AC于点F,若CF=5,sin∠CAD=![]() ,求线段BD的长.
,求线段BD的长.

参考答案:
【答案】(1)见解析;(2) ![]() .
.
【解析】分析:(1)连结OC交BD于点G.证明∠ECA+∠ACO=90°即可得到结论;
(2)设DF=3x,则AF=5x,AD=4x.由∠CAD=∠ACO,得到sin∠FCG=![]() .进而表示出BG,OG,OB.在Rt△OBG中,由勾股定理得到OB2=OG2+BG2,解方程即可得出结论.
.进而表示出BG,OG,OB.在Rt△OBG中,由勾股定理得到OB2=OG2+BG2,解方程即可得出结论.
详解:(1)连结OC交BD于点G.
∵AC平分∠BAD,∴∠CAD=∠CAB.
又∵OA=OC,∴∠CAB=∠ACO.
又∵CE⊥AD, ∴∠E=90°,∴∠EAC+∠ECA=90°,
∴∠ECA+∠ACO=90°,∴CE为⊙O的切线.
(2)设DF=3x,则AF=5x,AD=4x.
又∵AB为⊙O的直径,∴∠ADB=90°,∴BD∥CE,∴OC⊥BD.
又∵∠CAD=∠ACO,∴sin∠FCG=![]() .
.
又∵CF=5,∴CG=4,FG=3,∴DG=BG=3x+3.
又∵OC∥AE,∴OG=![]() AD=2x,∴OC=OB=4+2x.
AD=2x,∴OC=OB=4+2x.
在Rt△OBG中,OB2=OG2+BG2,∴(4+2x)2=(2x)2+(3x+3)2 ,
∴x=![]() 或-1.
或-1.
又∵x>0,∴x=![]() ,∴BD=2BG=
,∴BD=2BG=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
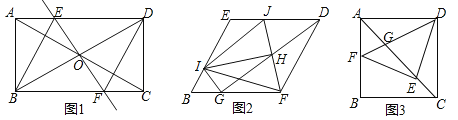
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b交x轴于点A(1,0),与双曲线y=-
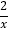 (x<0)交于点B(-1,a).
(x<0)交于点B(-1,a).(1)求直线AB的解析式;
(2)若点B左侧一直线x=m与直线AB交于点C,与双曲线交于点D(C、D两点不重合),当BC=BD时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0.
(1)试判断原方程根的情况;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.
(友情提示:AB=|x2﹣x1|)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC=2
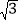 ,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.
,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F.(1)如图1,当点E′与点F重合时,求证:四边形ABE′C为平行四边形;
(2)如图2,延长ED交线段BF于点G.
①设BG=x,GF=y,求y与x的函数关系式;
②若△DFG的面积为3
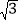 ,求AE的长.
,求AE的长.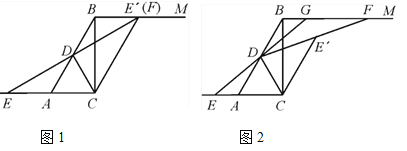
相关试题

