【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

参考答案:
【答案】(1)0回到球线上;(2)19米;(3)三次
【解析】试题(1)根据有理数的加法,可得答案;
(2)根据有理数的加法,可得每次与球门线的距离,根据有理数的大小比较,可得答案;
(3)根据有理数的大小比较,可得答案.
试题解析:(1)+10-2+5-6+12-9+4-14=0,
答:守门员最后正好回到球门线上;
(2)第一次10,第二次10-2=8,第三次8+5=13,第四次13-6=7,第五次7+12=19,第六次19-9=10,第七次10+4=14,第八次14-14=0,
19>14>13>10>8>7,
答:守门员离开球门线的最远距离达19米;
(3)第一次10=10,第二次10-2=8<10,第三次8+5=13>10,第四次13-6=7<10,第五次7+12=19>10,第六次19-9=10,第七次10+4=14>10,第八次14-14=0,
答:对方球员有三次挑射破门的机会.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)x(x-1)=3x+7
(2)4x2-4x+1=(x+3)2 -
科目: 来源: 题型:
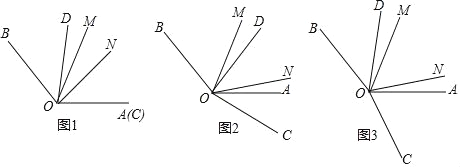
查看答案和解析>>【题目】已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.
(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,
①∠MON与旋转度数n°有怎样的数量关系?说明理由;
②当n为多少时,∠MON为直角?
(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OC绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
 请你根据上图填写下表:
请你根据上图填写下表:销售公司
平均数
方差
中位数
众数
甲
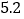
9
乙
9

8
 请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析: 从平均数和方差结合看;
从平均数和方差结合看; 从折线图上甲、乙两个汽车销售公司销售数量的趋势看
从折线图上甲、乙两个汽车销售公司销售数量的趋势看 分析哪个汽车销售公司较有潜力
分析哪个汽车销售公司较有潜力 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
 ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
ABC的三个顶点的坐标分别为A(-1,1), B(-3,1),C(-1,4).
①画出△ABC关于y轴对称的△A1B1C1;
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】诸暨某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
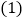 设每件童装降价x元时,每天可销售______件,每件盈利______元;
设每件童装降价x元时,每天可销售______件,每件盈利______元; 用x的代数式表示
用x的代数式表示
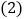 每件童装降价多少元时,平均每天赢利1200元.
每件童装降价多少元时,平均每天赢利1200元.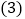 要想平均每天赢利2000元,可能吗?请说明理由.
要想平均每天赢利2000元,可能吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值
相关试题

