【题目】如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A'B'C'的位置后,再沿CB方向向左平移,使点B'落在原三角板ABC的斜边AB上,则三角板A'B'C'平移的距离为( )
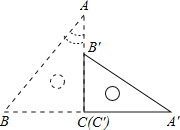
A.6cm B.4cm C.(6﹣![]() )cm D.(
)cm D.(![]() )cm
)cm
参考答案:
【答案】C
【解析】
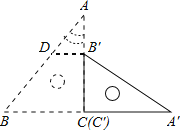
试题分析:如图,过B′作B′D⊥AC,垂足为B′,则三角板A'B'C'平移的距离为B′D的长,根据AB′=AC﹣B′C,∠A=30°,在Rt△AB′D中,解直角三角形求B′D即可.
解:如图,过B′作B′D⊥AC,垂足为B′,
∵在Rt△ABC中,AB=12,∠A=30°,
∴BC=![]() AB=6,AC=ABcos30°=6
AB=6,AC=ABcos30°=6![]() ,
,
由旋转的性质可知B′C=BC=6,
∴AB′=AC﹣B′C=6![]() ﹣6,
﹣6,
在Rt△AB′D中,∵∠A=30°,
∴B′D=AB′tan30°=(6![]() ﹣6)×
﹣6)×![]() =(6﹣2
=(6﹣2![]() )cm.
)cm.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点N是AB上一点,且BN=2AN,AC、DN相交于点M,则S△ADM:S四边形CMNB的值为( )
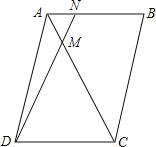
A.3:11 B.1:3 C.1:9 D.3:10
-
科目: 来源: 题型:
查看答案和解析>>【题目】说法中,不正确的是( )
A. 棱柱的侧面可以是三角形;
B. 棱柱的侧面展开图是一个长方形;
C. 若一个棱柱的底面为5边形、则可知该棱柱侧面是由5个长方形组成的;
D. 棱柱的上底面与下底面的形状与大小是完全一样的。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题:①坐标平面内的点与有序数对一一对应;②若a大于0,b不大于0,则点P(-a,-b)在第三象限;③在x轴上的点的纵坐标都为0;
④当m=0时,点P(m,-m)在第四象限。其中,是真命题的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥CD,∠C=115°,∠A=25°,则∠E=( )
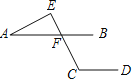
A.70° B.80° C.90° D.100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,AC⊥AB,AB=
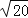 ,且AC:BD=2:3.
,且AC:BD=2:3.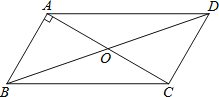
(1)求AC的长;
(2)求△AOD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x<﹣6的解集为( )
A.x<﹣3 B.x>﹣3 C.x>3 D.x<3
相关试题

