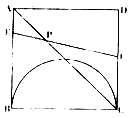
【题目】如图,正方形![]() 中,以
中,以![]() 为直径作半圆,
为直径作半圆,![]() .现有两动点
.现有两动点![]() 、
、![]() ,分别从点
,分别从点![]() 、点
、点![]() 同时出发,点
同时出发,点![]() 沿线段
沿线段![]() 以
以![]() /秒的速度向点
/秒的速度向点![]() 运动,点
运动,点![]() 沿折线
沿折线![]() 以
以![]() /秒的速度向点
/秒的速度向点![]() 运动.当点
运动.当点![]() 到达
到达![]() 点时,
点时,![]() 、
、![]() 同时停止运动,设点
同时停止运动,设点![]() 运动时间为
运动时间为![]() .
.

(1)当![]() 为何值时,线段
为何值时,线段![]() 与
与![]() 平行?
平行?
(2)设![]() ,当
,当![]() 为何值时,
为何值时,![]() 与半圆相切?
与半圆相切?
(3)如图2,将图形放在直角坐标系中,当![]() 时,设
时,设![]() 与
与![]() 相交于点
相交于点![]() ,双曲线
,双曲线![]() 经过点
经过点![]() ,并且与边
,并且与边![]() 交于点
交于点![]() ,求出双曲线的函数关系式,并直接写出
,求出双曲线的函数关系式,并直接写出![]() 的值.
的值.
参考答案:
【答案】(1)、t=![]() ;(2)、t=
;(2)、t=![]() ;(3)、y=-
;(3)、y=-![]() ;
;![]() .
.
【解析】
试题分析:(1)、设时间为t,则BE=t,CF=4-2t,根据BE=CF求出t的值;(2)、设时间为t,过F点作FK∥BC,交AB于K,则BE=t,CF=4-2t,EK=3t-4,EF=4-t,根据Rt△EKF的勾股定理求出t的值,得出答案;(3)、根据题意得出![]() ,根据△APE∽△CPE得出
,根据△APE∽△CPE得出![]() ,从而说明点P的位置与t的数值无关,根据AC的长度求出CP的长度,从而得出点P的坐标,利用待定系数法求出函数解析式,得出点H的坐标,从而得出答案.
,从而说明点P的位置与t的数值无关,根据AC的长度求出CP的长度,从而得出点P的坐标,利用待定系数法求出函数解析式,得出点H的坐标,从而得出答案.
试题解析:(1)、设E、F出发后经过t秒时,EF∥BC,
此时BE=t,CF=4-2t,BE=CF,即t=4-2t,∴![]()
(2)、设E、F出发后t秒时,EF与半圆相切,过F点作FK∥BC,交AB于K.
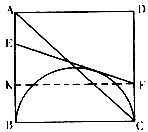
则BE=t,CF=4-2t,EK=EB-KB=EB-FC=t-(4-2t)=3t-4 EF=BE+CF(切线长相等)=4-t
在Rt△EKF中,EF2=EK2+KF2=(4-t)2=(3t-4)2+22 解得:![]() 或
或![]() (舍去)
(舍去)
(3)、当1<t<2时,如图:由![]()
∴AB∥DC,∴△APE∽△CPE 则![]() 即点P的位置与t的数值无关.
即点P的位置与t的数值无关.
点P的位置不会发生变化,AP∶PC的值为![]() 可求
可求![]() ,由AP∶PC=1:2可得CP=
,由AP∶PC=1:2可得CP=![]()
∴P(![]() )设双曲线解析式为
)设双曲线解析式为![]() ,将P(
,将P(![]() ) 代入得
) 代入得![]() ,∴
,∴![]()
∴H(![]() ) 得
) 得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.
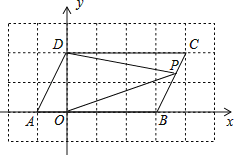
(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动的开展情况,随机抽查了全市七年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题:
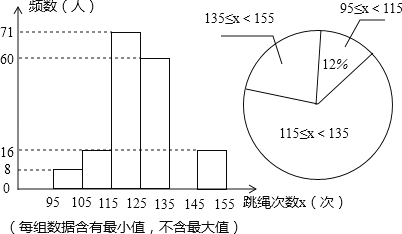
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,其中扇形统计图中表示跳绳次数范围135≤x<155的扇形的圆心角度数为 度.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市28000名七年级学生中有多少名学生的成绩为优秀?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
 的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3)
的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3)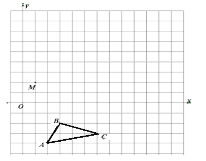
(1)画出△ABC关于
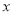 轴对称的△A1B1C1;
轴对称的△A1B1C1;(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 ,使△A2B2C2与△A1B1C1的相似比为2:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋子中装有大小完全相同的3粒乒乓球,其中2粒白色,1粒黄色.请你用它为甲、乙两位同学设计一个能决定胜负的公平的摸球游戏规则.并说明公平的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一个运算流程.

(1)分别计算:当x=150时,输出值为 ,当x=27时,输出值为 ;
(2)若需要经过两次运算,才能运算出y,求x的取值范围;
(3)请给出一个x的值,使之无论运算多少次都不能输出,并请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】4的算术平方根是( )
A.4
B.2
C.﹣2
D.±2
相关试题

