【题目】如图,已知△ABC中,AB=BC=5,tan∠ABC=![]() .
.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求![]() 的值.
的值.

参考答案:
【答案】(1)AC=![]() ;(2)
;(2)![]() .
.
【解析】(1)过A作AE⊥BC,在直角三角形ABE中,利用锐角三角函数定义求出AC的长即可;
(2)由DF垂直平分BC,求出BF的长,利用锐角三角函数定义求出DF的长,利用勾股定理求出BD的长,进而求出AD的长,即可求出所求.
(1)如图,过点A作AE⊥BC,
在Rt△ABE中,tan∠ABC=![]() ,AB=5,
,AB=5,
∴AE=3,BE=4,
∴CE=BC﹣BE=5﹣4=1,
在Rt△AEC中,根据勾股定理得:AC=![]() =
=![]() ;
;
(2)∵DF垂直平分BC,
∴BD=CD,BF=CF=![]() ,
,
∵tan∠DBF=![]() ,
,
∴DF=![]() ,
,
在Rt△BFD中,根据勾股定理得:BD=![]() =
=![]() ,
,
∴AD=5﹣![]() =
=![]() ,
,
则![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,试解决下列问题:
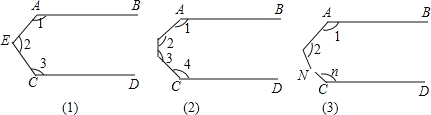
(1)图(1)中,∠1+∠2+∠3= ;
(2)图(2)中,∠1+∠2+∠3+∠4= ;
(3)图(3)中,∠1+∠2+∠3+…+∠n= .
-
科目: 来源: 题型:
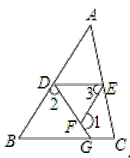
查看答案和解析>>【题目】完成下列推理过程:
已知:如图,∠1+∠2=180°,∠3=∠B
求证:∠EDG+∠DGC=180°
证明:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°( )
∴∠2= ( )
∴EF∥AB( )
∴∠3= ( )
又∵∠3=∠B(已知)
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG+∠DGC=180°( )
-
科目: 来源: 题型:
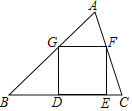
查看答案和解析>>【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)化简求值:(a-b)(a+b)+a(2b-a),其中a=
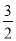 ,b=-2
,b=-2(2)已知x2-2x=1,求(x-1)(3x+1)-(x+1)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC中,E是线段AC上一点,F是BC延长线上一点.连接BE,AF.点G是线段BE的中点,BN∥AC,BN与AG延长线交于点N.
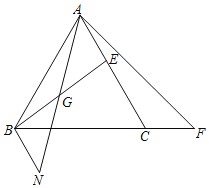
(1)若∠BAN=15°,求∠N;
(2)若AE=CF,求证:2AG=AF.
相关试题

