【题目】如图,等边三角形ABC中,E是线段AC上一点,F是BC延长线上一点.连接BE,AF.点G是线段BE的中点,BN∥AC,BN与AG延长线交于点N.
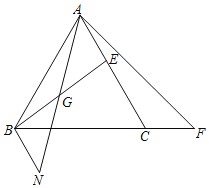
(1)若∠BAN=15°,求∠N;
(2)若AE=CF,求证:2AG=AF.
参考答案:
【答案】(1)45°;(2)见解析
【解析】
(1)由等边三角形的性质可知∠ABC=∠ACB=60°,由平行线的性质可知∠NBC=60°,进一步求出∠ABN=120°,再由三角形内角和定理即可求出∠N的度数;
(2)先证△NBG≌△AEG,得到AG=NG,AE=BN,再证△ABN≌△ACF,即可推出AF=2AG.
解:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵AC∥BN,
∴∠NBC=∠ACB=60°,
∴∠ABN=∠ABC+∠NBC=120°,
∴在△ABN中,
∠N=180°﹣∠ABN﹣∠BAN=180°﹣120°﹣15°=45°;
(2)∵AC∥BN,
∴∠N=∠GAE,∠NBG=∠AEG,
又∵点G是线段BE的中点,
∴BG=EG,
∴△NBG≌△AEG(AAS),
∴AG=NG,AE=BN,
∵AE=CF,
∴BN=CF,
∵∠ACB=60°,
∴∠ACF=180°﹣∠ACB=120°,
∴∠ABN=∠ACF,
又∵AB=AC,
∴△ABN≌△ACF(SAS),
∴AF=AN,
∵AG=NG=![]() AN,
AN,
∴AF=2AG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=BC=5,tan∠ABC=
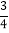 .
.(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求
 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)化简求值:(a-b)(a+b)+a(2b-a),其中a=
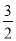 ,b=-2
,b=-2(2)已知x2-2x=1,求(x-1)(3x+1)-(x+1)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课
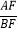 =
=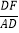 .求证:EF=EP.
.求证:EF=EP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.

(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:△MNC是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,分别过点B、C两点作过点A的直线的垂线,垂足为M、N.

(1)如图1,当M、N两点在直线BC的同侧时,求证:BM+CN=MN;
(2)如图2,当M、N两点在直线BC的两侧时,BM、CN、MN三条线段的数量关系并证明.
相关试题

