【题目】在正方形网格中,我们把,每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,在下列如图所示的正方形网格中,每个小正方形的边长为1. 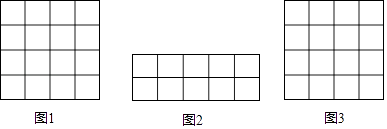
(1)请你在图1中画一个格点图形,且该图形是边长为 ![]() 的菱形;
的菱形;
(2)请你在图2中用网格线段将其切割成若干个三角形和正方形,拼接成一个与其面积相等的正方形,并在图3中画出格点正方形.
参考答案:
【答案】
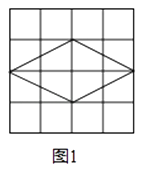
(1)解:如图1所示:四边形即为菱形
(2)解:如图2,3所示:即为所求答案
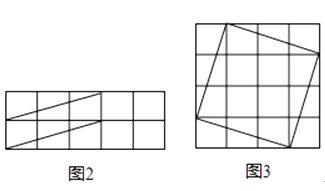
【解析】(1)直接利用菱形的性质结合其面积得出答案;(2)利用正方形的性质结合正方形面积求法得出答案.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算:(﹣1)3﹣( )﹣2×
)﹣2×  +6×|﹣
+6×|﹣  |
|
(2)化简并求值:( )÷
)÷  ,其中a=1,b=2.
,其中a=1,b=2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD 是一段斜坡,AB 是水平线,现为了测斜坡上一点 D 的铅直高度(即 垂线段 DB 的长度),小亮在点 D 处立上一竹竿 CD,并保证 CD=AB,CD⊥AD,然后在竿顶 C 处垂下一根细绳(细绳末端挂一重锤,以使细绳与水平线垂直),细绳与斜坡 AD 交于点E,此时他测得 CE=8 m,AE=6 m,求 BD 的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):学生孝敬父母情况统计表:
选项
频数
频率
A
m
0.15
B
60
p
C
n
0.4
D
48
0.2
根据以上信息解答下列问题:
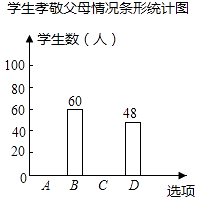
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)的图象是( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
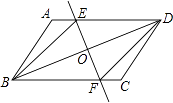
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由. -
科目: 来源: 题型:
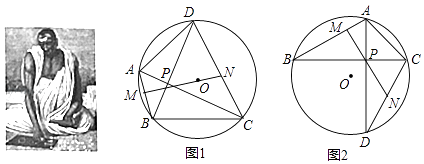
查看答案和解析>>【题目】阅读与思考 婆罗摩笈多(Brahmagupta),是一位印度数学家和天文学家,书写了两部关于数学和天文学的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数概念及加减法运算仅晚于中国《九章算术》,而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及部分证明过程如下:
已知:如图1,四边形ABCD内接于⊙O,对角线AC⊥BD于点P,PM⊥AB于点M,延长MP交CD于点N,求证:CN=DN.
证明:在△ABP和△BMP中,∵AC⊥BD,PM⊥AB,
∴∠BAP+∠ABP=90°,∠BPM+∠MBP=90°.
∴∠BAP=∠BPM.
∵∠DPN=∠BPM,∠BAP=∠BDC.
∴…
(1)请你阅读婆罗摩笈多定理的证明过程,完成剩余的证明部分.
(2)已知:如图2,△ABC内接于⊙O,∠B=30°,∠ACB=45°,AB=2,点D在⊙O上,∠BCD=60°,连接AD,与BC交于点P,作PM⊥AB于点M,延长MP交CD于点N,则PN的长为 .
相关试题

