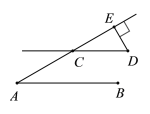
【题目】(1)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=30°,求∠D的度数.
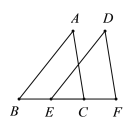
(2)如图,E,C在BF上,AB=DE,AC=DF,BE=CF,试说明:AC∥DF.
参考答案:
【答案】(1)53°;(2)证明见解析
【解析】
(1)运用平行线性质,及三角形内角和定理可求得;(2)证△ABC≌△DEF
得∠ACB=∠F,故AC∥DF.
(1)解: ∵AB∥CD
∴∠ECD=∠A=37°(两直线平行,同位角相等)
∵在△CDE中,DE⊥AE
∴∠CED=90°
∴∠D=180°-∠ECD-∠CED=180°-90°-37°=53°
(2)∵BE=CF,
∴BC=EF
在△ABC和△DEF中
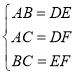
∴△ABC≌△DEF
∴∠ACB=∠F
∴AC∥DF
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低
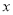 元,则每天的销售量是__________斤(用含
元,则每天的销售量是__________斤(用含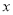 的代数式表示);
的代数式表示);(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 和△BDE 都是等边三角形,A、B、D 三点共线.下列结论:①AB=CD;②BF=BG;③HB 平分∠AHD;④∠AHC=60°,⑤△BFG 是等边三角形.其中正确的有____________(只填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了
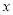 秒.
秒.(1)当
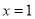 时,求PC的长;
时,求PC的长;(2)当
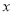 为何值时,△NPC是以PC为腰的等腰三角形?
为何值时,△NPC是以PC为腰的等腰三角形?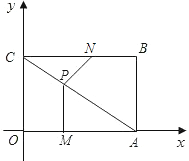
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
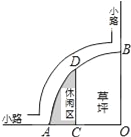
A. (10π﹣
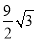 )米2 B. (π﹣
)米2 B. (π﹣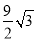 )米2 C. (6π﹣
)米2 C. (6π﹣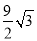 )米2 D. (6π﹣
)米2 D. (6π﹣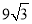 )米2
)米2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
 ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
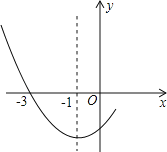
A. ①② B. ②③ C. ①②④ D. ②③④
相关试题

