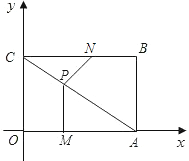
【题目】如图,矩形OABC的顶点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了![]() 秒.
秒.
(1)当![]() 时,求PC的长;
时,求PC的长;
(2)当![]() 为何值时,△NPC是以PC为腰的等腰三角形?
为何值时,△NPC是以PC为腰的等腰三角形?
参考答案:
【答案】(1)当![]() 时,
时, ![]() ;(2)当
;(2)当![]() 或
或![]() 时,△NPC是以PC为腰的等腰三角形.
时,△NPC是以PC为腰的等腰三角形.
【解析】试题分析:(1)利用平行于三角形底边所构成对应边成比例得到![]() ,代入数据求值.(2)随着M,N点的运动,当PC=PN时, 利用矩形的性质,BC=CN+BN,求得x值 ;当PC=CN时,列出对应边成比例
,代入数据求值.(2)随着M,N点的运动,当PC=PN时, 利用矩形的性质,BC=CN+BN,求得x值 ;当PC=CN时,列出对应边成比例![]() ,代入求值.
,代入求值.
试题解析:
(1)∵ 点A(4,0),B(4,3),∴ OA=4,AB=3,
在矩形OABC中,BC=OA=4,OC=AB=3,∠AOC=∠BCO=90°,
在Rt△AOC中, ![]() ,
,
依题知:OM=BN=![]() =1,又PM⊥OA ,∴ PM∥OC,
=1,又PM⊥OA ,∴ PM∥OC,
∴![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ 当![]() 时,
时, ![]() .
.
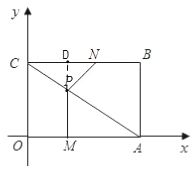
(2)①当PC=PN时,△NPC是以PC为腰的等腰三角形,
延长MP交BC于点为D,
在矩形OABC中,BC∥OA ,∴ PD⊥BC ,
又∠AOC=∠BCO=90°,
∴ 四边形OCDM为矩形 ,∴ CD=OM=![]() ,
,
又PC=PN,PD⊥BC ,∴ CN=2CD=![]() ,
,
∵ BC=CN+BN ,∴ ![]() ,∴
,∴ ![]() ,
,
∴ 当![]() 时,△NPC是以PC为腰的等腰三角形.
时,△NPC是以PC为腰的等腰三角形.
② 当PC=CN时,△NPC是以PC为腰的等腰三角形,
由上面知:CN=BC-BN=![]() =PC, ∵ PM∥OC ,
=PC, ∵ PM∥OC ,
∴![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
∴ 当![]() 时,△NPC是以PC为腰的等腰三角形;
时,△NPC是以PC为腰的等腰三角形;
综上所述,当![]() 或
或![]() 时,△NPC是以PC为腰的等腰三角形.
时,△NPC是以PC为腰的等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低
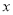 元,则每天的销售量是__________斤(用含
元,则每天的销售量是__________斤(用含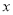 的代数式表示);
的代数式表示);(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 和△BDE 都是等边三角形,A、B、D 三点共线.下列结论:①AB=CD;②BF=BG;③HB 平分∠AHD;④∠AHC=60°,⑤△BFG 是等边三角形.其中正确的有____________(只填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=30°,求∠D的度数.
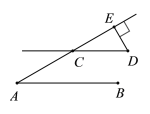
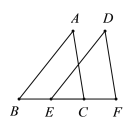
(2)如图,E,C在BF上,AB=DE,AC=DF,BE=CF,试说明:AC∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
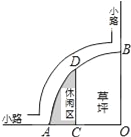
A. (10π﹣
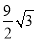 )米2 B. (π﹣
)米2 B. (π﹣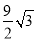 )米2 C. (6π﹣
)米2 C. (6π﹣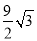 )米2 D. (6π﹣
)米2 D. (6π﹣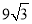 )米2
)米2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
 ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
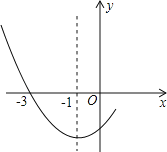
A. ①② B. ②③ C. ①②④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:(不要求写作法)如图,在 10×10 的方格纸中,有一个格点四边形 ABCD(即四边形的顶点都在格点上)。①在给出的方格纸中,画出四边形 ABCD 向下平移 5 格后的四边形 A
 B
B C
C D
D ;②在给出的方格纸中,画出四边形 ABCD 关于直线 l 对称的图形 A
;②在给出的方格纸中,画出四边形 ABCD 关于直线 l 对称的图形 A B
B C
C D
D .
.
相关试题

