【题目】已知关于x的一元二次方程x2+(2m+1)x+m2-4=0.
(1)当m为何值时,方程有两个不相等的实数根?
(2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.
参考答案:
【答案】(1)当m>-![]() 时,方程有两个不相等的实数根;(2)m的值为-4.
时,方程有两个不相等的实数根;(2)m的值为-4.
【解析】试题分析:(1)根据方程的系数结合根的判别式,即可得出![]() 解之即可得出结论;
解之即可得出结论;
(2)设方程的两根分别为![]() 根据根与系数的关系结合菱形的性质,即可得出关于
根据根与系数的关系结合菱形的性质,即可得出关于![]() 的一元二次方程,解之即可得出
的一元二次方程,解之即可得出![]() 的值,再根据
的值,再根据![]() 即可确定
即可确定![]() 的值.
的值.
试题解析:(1)∵方程![]() 有两个不相等的实数根,
有两个不相等的实数根,
![]()
解得: ![]()
∴当![]() 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根.
(2)设方程的两根分别为a、b,
根据题意得: ![]()
∵2a、2b为边长为5的菱形的两条对角线的长,
![]()
解得:m=4或m=2.
∵a>0,b>0,
∴a+b=2m1>0,
∴m=4.
若边长为5的菱形的两条对角线的长分别为方程两根的2倍,则m的值为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(0,1)、B(3,3)、C(1,3).

(1) 画出△ABC关于点O的中心对称图形△A1B1C1
(2) 画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为______.
(3) 若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿.如果分给每位儿童5盒牛奶,那么剩下18盒牛奶;如果分给每位儿童6盒牛奶,那么最后一位儿童分不到6盒,但至少能有3盒.则这个儿童福利院的儿童最少有________个,最多有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
-
科目: 来源: 题型:
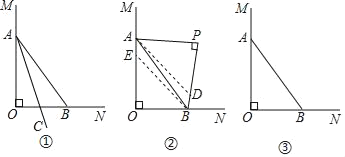
查看答案和解析>>【题目】如图,已知OM⊥ON,垂足为O,点A、B分别是射线OM、ON上的一点(O点除外).
(1)如图①,射线AC平分∠OAB,是否存在点C,使得BC所在的直线也平分以B为顶点的某一个角α(0°<α<180°),若存在,则∠ACB= ;
(2)如图②,P为平面上一点(O点除外),∠APB=90°,且OA≠AP,分别画∠OAP、∠OBP的平分线AD、BE,交BP、OA于点D、E,试简要说明AD∥BE的理由;
(3)在(2)的条件下,随着P点在平面内运动,AD、BE的位置关系是否发生变化?请利用图③画图探究,如果不变,直接回答;如果变化,画出图形并直接写出AD、BE位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) (-1)0+2-2-(-1)2012 (2)(2x2y)2 ·(-6xy4)÷(24x4y5)
(3)x 2-(x+2)(x-2) (4)(3-2x)(3+2x)+(2x-1)2
(5)(x-2)(x+2)-(x+1)(x-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,后求值
(1)(2a-3b)(3b+2a)-(a-2b)2,其中:a=-2,b=3;
(2)[(xy+2)(xy-2)-2x2y2+4]÷(xy),其中x=10,y=-
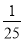 .
.
相关试题

