【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC于点F.
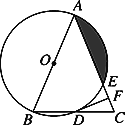
(1)判断DF与是⊙O的位置关系,并证明你的结论。
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
参考答案:
【答案】(1)详见解析;(2)4π-8.
【解析】试题分析:(1)连OD,AD,利用OD∥AC证明OD⊥DF.(2)利用扇形面积减去三角形面积求阴影部分面积.
试题解析:
(1)相切。证明:如图,连OD,AD,
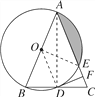
∵AB是⊙O的直径,∴AD⊥BC,
又∵AB=AC,∴D是BC的中点,
∵OA=OB∴OD是△ABC的中位线,
∴OD∥AC∵DF⊥AC, ∴OD⊥DF,
∴DF是⊙O的切线.
(2)解:∵∠CDF=22.5°,DF⊥AC,∴∠C=67.5°,
∴∠BAC=2∠DAC=45°,
连接OE,则∠BOE=2∠BAC=90°,∴∠AOE=90°,
∴S阴影=![]() ×4×4=4π-8.
×4×4=4π-8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC的平分线与∠ACD的平分线交于点A
 ,∠A
,∠A BC的平分线与∠A
BC的平分线与∠A CD的平分线交于点A
CD的平分线交于点A ,以此类推,∠A
,以此类推,∠A BC的平分线与∠A
BC的平分线与∠A CD的平分线交于点A
CD的平分线交于点A ,则∠A
,则∠A 的大小是___
的大小是___
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为等边三角形,
为等边三角形, ,
, 、
、 相交于点
相交于点 ,
, 于点
于点 ,
,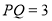 ,
, .
.(1)求证:
 ;
;(2)求
 的长.
的长.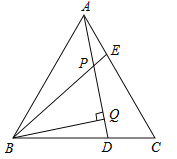
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE=
 OC;
OC;当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
(1)若BF⊥AE,
①求证:BF=AE;
②连接OD,确定OD与AB的数量关系,并证明;
(2)若正方形的边长为4,且BF=AE,求BO的长.

相关试题

