【题目】已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE=![]() OC;
OC;
当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.


参考答案:
【答案】图②中OD+OE=![]() OC成立.证明见解析;图③不成立,有数量关系:OE-OD=
OC成立.证明见解析;图③不成立,有数量关系:OE-OD=![]() OC
OC
【解析】试题分析:当三角板绕点C旋转到CD与OA不垂直时,易得△CKD≌△CHE,进而可得出证明;判断出结果.解此题的关键是根据题意找到全等三角形或等价关系,进而得出OC与OD、OE的关系;最后转化得到结论.
试题解析:图②中OD+OE=![]() OC成立.
OC成立.
证明:过点C分别作OA,OB的垂线,垂足分别为P,Q.
有△CPD≌△CQE,
∴DP=EQ,
∵OP=OD+DP,OQ=OE-EQ,
又∵OP+OQ=![]() OC,
OC,
即OD+DP+OE-EQ=![]() OC,
OC,
∴OD+OE=![]() OC.
OC.
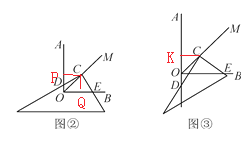
图③不成立,
有数量关系:OE-OD=![]() OC
OC
过点C分别作CK⊥OA,
CH⊥OB,
∵OC为∠AOB的角平分线,且CK⊥OA,CH⊥OB,
∴CK=CH,∠CKD=∠CHE=90°,
又∵∠KCD与∠HCE都为旋转角,
∴∠KCD=∠HCE,
∴△CKD≌△CHE,
∴DK=EH,
∴OE-OD=OH+EH-OD=OH+DK-OD=OH+OK,
由(1)知:OH+OK=![]() OC,
OC,
∴OD,OE,OC满足OE-OD=![]() OC.
OC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC于点F.
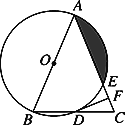
(1)判断DF与是⊙O的位置关系,并证明你的结论。
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为等边三角形,
为等边三角形, ,
, 、
、 相交于点
相交于点 ,
, 于点
于点 ,
,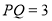 ,
, .
.(1)求证:
 ;
;(2)求
 的长.
的长.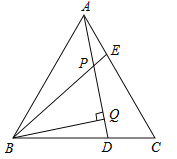
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
(1)若BF⊥AE,
①求证:BF=AE;
②连接OD,确定OD与AB的数量关系,并证明;
(2)若正方形的边长为4,且BF=AE,求BO的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在8×8的网格中的每个小正方形边长都是1,线段交点称作格点.任意连接这些格点,可得到一些线段.按要求作图:
(1)请画出△ABC的高AD;
(2)请连接格点,用一条线段将图中△ABC分成面积相等的两部分;
(3)直接写出△ABC的面积是_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠CBF为( )
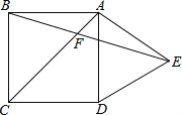
A.75°B.60°C.55°D.45°
相关试题

