Question

【题目】如图所示，抛物线y=ax2+bx+c与直线y=﹣x+6分别交于x轴和y轴上同一点，交点分别是点B和点C，且抛物线的对称轴为直线x=4．

（1）求出抛物线与x轴的两个交点A，B的坐标．
（2）试确定抛物线的解析式．

Answer 1

【答案】
（1）解：∵抛物线y=ax2+bx+c与直线y=﹣x+6分别交于x轴和y轴上同一点，交点分别是点B和点C，

∴将x=0代入y=﹣x+6得，y=6；将y=0代入y=﹣x+6，得x=6．

∴点B的坐标是（6，0），点C的坐标是（0，6）．

∵抛物线y=ax2+bx+c与x轴交于点A、B两点，对称轴为直线x=4，

∴点A的坐标为（2，0）．

即抛物线与x轴的两个交点A，B的坐标分别是（2，0），（6，0）．

（2）解：∵抛物线y=ax2+bx+c过点A（2，0），B（6，0），C（0，6），

∴

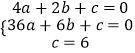
解得a= ，b=﹣4，c=6．

∴抛物线的解析式为：y=

【解析】先求出B坐标，由对称轴的意义，可知对称轴与x轴交点就是AB的中点，可求出B点坐标，进而求出解析式.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识，掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．