【题目】如图,OE平分∠AOB,且EC⊥OA,ED⊥OB,垂足分别是C,D,连结CD与OE交于点F.
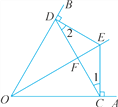
(1)求证:∠1=∠2.
(2)求证:OE是线段CD的垂直平分线.
(3)若∠1=30°,OC=2,求△OCD与△CDE的面积之差.
参考答案:
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】试题分析:(1)根据角平分线上的点到角的两边的距离相等可得CE=DE,然后根据等边对等角证明即可;
(2)利用“HL”证明△OCE和△ODE全等,根据全等三角形对应边相等可得OC=OD,再根据到线段两端点距离相等的点在线段垂直平分线上证明.
(3)分别求出ΔOCD和ΔCDE的面积即可求出△OCD与△CDE的面积之差.
试题解析:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴CE=DE,∴∠1=∠2.
(2)在Rt△OCE和Rt△ODE中,
∵![]()
∴Rt△OCE≌Rt△ODE(HL).
∴OC=OD.
又∵CE=DE,
∴OE是线段CD的垂直平分线.
(3)∵∠1=30°,∠OCE=90°,
∴∠OCD=60°.
∵OC=OD,
∴△OCD是边长为2的等边三角形,
∴CD=OC=2,∠COD=60°,
∴∠COE=∠DOE=![]() ∠COD=30°,
∠COD=30°,
∴OE=2CE.
设CE=x,则OE=2x.
由勾股定理,得(2x)2=x2+22,
解得x=![]() ,即CE=
,即CE=![]() ,OE=
,OE=![]() .
.
∵∠1=30°,∠EFC=90°,
∴EF=![]() CE=
CE=![]() ,∴OF=OE-EF=
,∴OF=OE-EF=![]() ,
,
∴S△OCD-S△CDE=![]() ·CD·OF-
·CD·OF-![]() ·CD·EF=
·CD·EF=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将抛物线y=x2+2向右平移1个单位,那么所得新抛物线的表达式是( )
A.y=x2+3
B.y=(x﹣1)2+2
C.y=(x+1)2+2
D.y=x2+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(10x﹣31)(13x﹣17)﹣(13x﹣17)(3x﹣23)可因式分解成(ax+b)(7x+c),其中a、b、c均为整数,求a+b+c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,F为BE的中点,连结DF,CF.
(1)如图①,当点D在AB上,点E在AC上,请直接写出此时线段DF,CF的数量关系和位置关系.
(2)如图②,在(1)的条件下将△ADE绕点A顺时针旋转45°,请你判断此时(1)中的结论是否仍然成立,并证明你的判断.
(3)如图③,在(1)的条件下将△ADE绕点A顺时针旋转90°,若AD=1,AC=2
 ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△AOB中,C,D分别是OA,OB边上的点,将△OCD绕点O顺时针旋转到△OC′D′.
(1)如图1,若∠AOB=90°,OA=OB,C,D分别为OA,OB的中点,证明:①AC′=BD′;②AC′⊥BD′;
(2)如图2,若△AOB为任意三角形且∠AOB=θ,CD∥AB,AC′与BD′交于点E,猜想∠AEB=θ是否成立?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在5×6的方格图中
在图1中,将线段A1A2向右平移1个单位到B1B2 , 得到封闭图形A1A2B2B1(即阴影部分)
在图2中,将线段A1A2A3向右平移1个单位到B1B2B3 , 得到封闭图形A1A2A3B3B2B1(即阴影部分)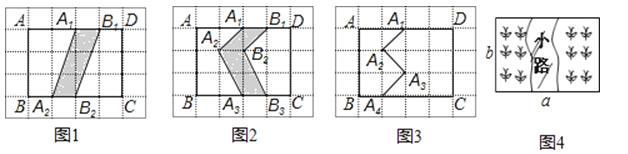
(1)在图3中,画出将折线A1A2A3A4向右平移1单位后的图形,并用阴影画出由这两条折线所围成的封闭图形.
(2)设上述三个图形中,矩形ABCD分别除去阴影部分后剩余部分的面积记为S1、S2、S3 , 则S1= ,S2= S3=
(3)如图4,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想草地部分的面积是 .(用含a、b的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2﹣(k+3)x+2k+2=0的根的情况,下面判断正确的是( )
A.有两个相等的实数根B.有两个不相等的实数根C.有两个实数根D.无实数根
相关试题

