【题目】如图,点O是△ABC边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;

参考答案:
【答案】(1)证明见解析;(2)5.
【解析】试题分析:(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案; (2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可得出CO的长.
试题解析:
(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6,
∵MN∥BC,
∴∠1=∠5,3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF=![]()
∴OC=EF=5;

-
科目: 来源: 题型:
查看答案和解析>>【题目】“等边三角形三条边相等”的逆命题是_____(填正确或者错误)
-
科目: 来源: 题型:
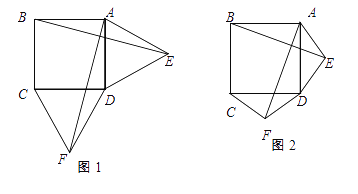
查看答案和解析>>【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(Ⅰ)请写出AF与BE的数量关系与位置关系分别是什么,并证明.
(Ⅱ)如图2,若将条件“两个等边三角形ADE和DCF”变为两个等腰三角形ADE和DCF,且EA=ED=FD=FC,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在全国各地都受到欢迎,今年某县在农村地区广泛推广,商家抓住机遇,某商场计划用3800元购进甲、乙两种型号的节能灯共120只,这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)求甲、乙两种节能灯各购进多少只?
(2)由于节能灯的销售量很好,商场在甲种型号节能灯销售一半后,将甲种节能灯的售价提高20%,如果商场把这120只节能灯全部销售完,那么该商场将获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣mx+3=0的解为﹣1,则m的值为( )
A. ﹣4 B. 4 C. ﹣2 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在比例尺为1∶50000的地图上,量得A、B两地的图上距离AB=3cm,则A、B两地的实际距离为____________ km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣4x+m的顶点在x轴上,则m的值等于( )
A. 2 B. 4 C. 6 D. 8
相关试题

