【题目】[感知发现]:如图,是一个“猪手”图,AB∥CD,点E在两平行线之间,连接BE,DE ,我们发现:∠E=∠B+∠D
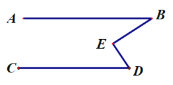
证明如下:过E点作EF∥AB.
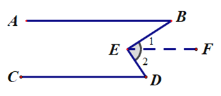
![]() ∠B=∠1(两直线平行,内错角相等.)
∠B=∠1(两直线平行,内错角相等.)
又![]() AB∥CD(已知)
AB∥CD(已知)
![]() CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
![]() ∠2=∠D(两直线平行,内错角相等.)
∠2=∠D(两直线平行,内错角相等.)
![]() ∠1+∠2=∠B+∠D(等式的性质1.)
∠1+∠2=∠B+∠D(等式的性质1.)
即:∠E=∠B+∠D
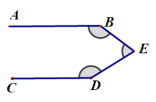
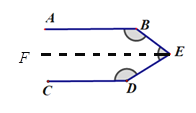
[类比探究]:如图是一个“子弹头”图,AB∥CD,点E在两平行线之间,连接BE,DE.试探究∠E+∠B+∠D=360°.写出证明过程.
[创新应用]:
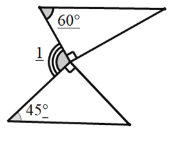
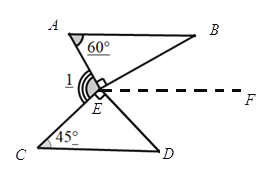
(1).如图一,是两块三角板按如图所示的方式摆放,使直角顶点重合,斜边平行,请直接写出∠1的度数.
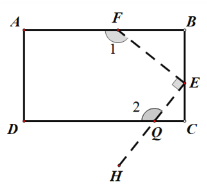
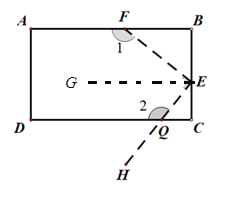
(2).如图二,将一个长方形ABCD按如图的虚线剪下,使∠1=120![]() ,∠FEQ=90°. 请直接写出∠2的度数.
,∠FEQ=90°. 请直接写出∠2的度数.
参考答案:
【答案】类比探究:见解析;
创新应用:(1):![]()
创新应用:(2):![]()
【解析】
[类比探究]:如图,过![]() 作
作![]() 结合已知条件得
结合已知条件得![]() 利用平行线的性质可得答案,
利用平行线的性质可得答案,
[创新应用]:
(1):由题意得:![]() 过
过![]() 作
作![]() 得到
得到![]() 利用平行线的性质可得答案,
利用平行线的性质可得答案,
(2):由题意得:![]() 过
过![]() 作
作![]() 得到
得到 ![]() 利用平行线的性质可得答案.
利用平行线的性质可得答案.
解:类比探究:如图,过![]() 作
作![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
[创新应用]:(1):由题意得:![]() 过
过![]() 作
作![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2):由题意得:![]() 过
过![]() 作
作![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() ∠1=120
∠1=120![]() ,∠FEQ=90°,
,∠FEQ=90°,
![]()
-
科目: 来源: 题型:
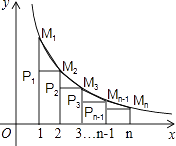
查看答案和解析>>【题目】已知反比例函数y=
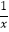 的图象,当x取1,2,3,…n时,对应在反比例图象上的点分别为M1、M2、M3…Mn , 则
的图象,当x取1,2,3,…n时,对应在反比例图象上的点分别为M1、M2、M3…Mn , 则 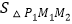 +
+ 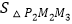 +…
+… 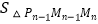 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角△ABC中,AD平分∠BAC交BC于点D,点M,N分别是AD和AB上的动点,当SABC=6,AC=4时,BM+MN的最小值等于_______。
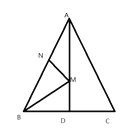
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC与BD相交于点O,点E是CD上的一点,F是OD上的一点,且EF∥AC,∠1=∠A.
(1)求证:AB∥CD.
(2)若∠BFE=70°,求:∠AOB的度数.
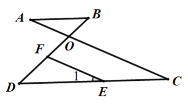
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(4,0)及在第一象限的动点P(x,y),且x+y=5,0为坐标原点,设△OPA的面积为S.
(1)求S关于x的函数表达式;
(2)求x的取值范围;
(3)当S=4时,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:长方形ABCD在坐标平面内的位置如图所示, A(1,1) C(-3,-4),点P从点A出发,沿着A→B→C→D→A的路径,以每秒
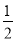 个单位的速度运动.运动一周回到A点时停止运动.设运动时间为t秒.
个单位的速度运动.运动一周回到A点时停止运动.设运动时间为t秒.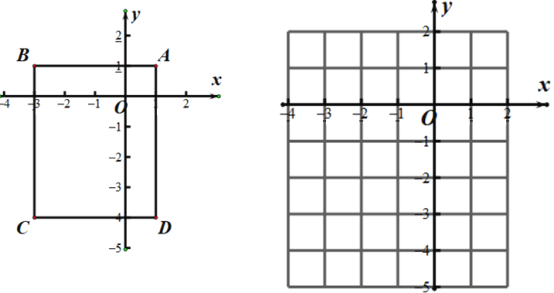
(1)直接写出点B、点D的坐标.
(2)当t=6秒时,写出P点的坐标.
(3)当点P运动到与x轴的距离为
 个单位时直接写出t的值.
个单位时直接写出t的值.
相关试题

