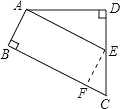
【题目】如图,四边形ABCD中,∠ADC=∠B=90°,∠C=60°,AD=![]() ,E为DC中点,AE∥BC.求BC的长和四边形ABCD的面积.
,E为DC中点,AE∥BC.求BC的长和四边形ABCD的面积.
参考答案:
【答案】BC=2.5;![]()
【解析】
试题分析:过E作EF⊥BC于F,证明四边形 ABCD是矩形,在Rt△ADE中求出AE,DE的长度,根据E是中点,求出EC的长度,继而求出CF,则可得出BC的长度,根据四边形ABCD的面积S四边形ABCD=S△ADE+S梯形ABCE也可求出其面积.
试题解析:过E作EF⊥BC于F,∵∠B=90°,∴AB∥EF,∵AE∥BC,∠B=90°,∴四边形 ABCD是矩形.
∵AE∥BC,∴∠AED=∠C=60°.在Rt△ADE中,∠ADC=90°,AD=![]() ,
,
∴DE=![]() =1,AE=
=1,AE=![]() =2,又∵E为DC中点,∴CE=DE=1,
=2,又∵E为DC中点,∴CE=DE=1,
在Rt△CEF中,∠CFE=90°,∠C=60°,则CF=CEcos 60°=![]() ,EF=CEsin 60°=
,EF=CEsin 60°=![]() ,
,
∴BC=BF+CF=AE+CF=2+![]() =
=![]() ,
,
∴四边形ABCD的面积S四边形ABCD=S△ADE+S梯形ABCE=![]() ADDE+
ADDE+![]() (AE+BC)EF=
(AE+BC)EF=![]() ×
×![]() ×1+
×1+![]() ×(2+
×(2+![]() )×
)×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A. 无法确定 B. 相切 C. 相交 D. 相离
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某文具店进行促销活动,决定将单价为a元的笔记本降价10%销售,降价后的销售价为( )
A. 10%a B. a-10% C. (1-10%)a D. (1+10%)a
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了利用尺规作一个角的平分线后,爱钻研的小聪发现,只有一把刻度尺也可以作出一个角的平分线.她是这样作的(如图):
(1)分别在∠AOB的两边OA,OB上各取一点C,D,使得OC=OD.
(2)连结CD,并量出CD的长度,取CD的中点E.
(3)过O,E两点作射线OE,则OE就是∠AOB的平分线.
请你说出小聪这样作的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
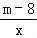 (m为常数)的图象经过点A(﹣1,6).
(m为常数)的图象经过点A(﹣1,6).(1)求m的值;
(2)如图,过点A作直线AC与函数y=
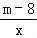 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.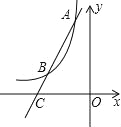
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=
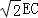 .其中正确结论的序号是( )
.其中正确结论的序号是( )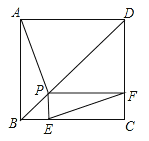
A. ①②③④ B. ①②④⑤ C. ②③④⑤ D. ①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】在中俄“海上联合﹣2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,
 1.7)
1.7)
相关试题

