【题目】如图,已知△ABC中,AB=AC,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法),并根据要求填空:
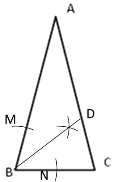
(1)作∠B的平分线BD,交AC于点D;
(2)作线段AB的垂直平分线EF,交AB于点E,交AC于点F;
(3)如果点F与点D重合,则∠A= °.

参考答案:
【答案】(1)见解析;(2)见解析;(3)36°
【解析】
(1)以B为圆心,以任意长度为半径作弧,分别交AB、BC与M、N,分别以M、N为圆心,以大于![]() MN为半径作弧,连接B和两弧的交点并延长交AC于D,BD即为所求;
MN为半径作弧,连接B和两弧的交点并延长交AC于D,BD即为所求;
(2)分别以A、B为圆心,以大于![]() AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,EF即为所求;
AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,EF即为所求;
(3)根据等边对等角可得:∠ABC=∠ACB,再根据角平分线的定义可得:∠ABC=2∠ABF,然后根据垂直平分线的性质和等边对等角可得:∠FBA=∠A,从而得出∠ACB=∠ABC=2∠A,最后根据三角形的内角和定理列方程即可求出∠A.
解:(1)以B为圆心,以任意长度为半径作弧,分别交AB、BC与M、N,分别以M、N为圆心,以大于![]() MN为半径作弧,连接B和两弧的交点并延长交AC于D,如下图所示,BD即为所求;
MN为半径作弧,连接B和两弧的交点并延长交AC于D,如下图所示,BD即为所求;
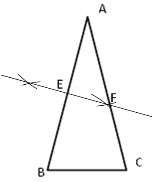
(2)分别以A、B为圆心,以大于![]() AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,如下图所示EF即为所求;
AB为半径作弧,连接两弧的两个交点交AB于E,交AC于F,如下图所示EF即为所求;
(3)当F、D重合时,如下图所示,
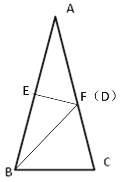
∵AB=AC
∴∠ABC=∠ACB
∵BF平分∠ABC
∴∠ABC=2∠ABF
∵EF垂直平分AB
∴FB=FA
∴∠FBA=∠A
∴∠ACB=∠ABC=2∠A
∵∠ACB+∠ABC+∠A=180°
∴2∠A+2∠A+∠A=180°
解得:∠A=36°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一组有规律的图案,第1个图案由4个
 组成,第2个图案由7个
组成,第2个图案由7个 组成,第3个图案由10个
组成,第3个图案由10个 组成,第4个图案由13个
组成,第4个图案由13个 组成,…,君君有100个
组成,…,君君有100个 ,她想按照这种规律组成一个最大的图案,则这个最大图案的一条边上的
,她想按照这种规律组成一个最大的图案,则这个最大图案的一条边上的 有____个.
有____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个口袋有
 个黑球和若干个白球,在不允许将球倒出来的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回口袋中,…,不断重复上述过程,小明共摸了
个黑球和若干个白球,在不允许将球倒出来的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回口袋中,…,不断重复上述过程,小明共摸了 次,其中
次,其中 次摸到黑球.根据上述数据,小明正估计口袋中的白球的个数是________.
次摸到黑球.根据上述数据,小明正估计口袋中的白球的个数是________. -
科目: 来源: 题型:
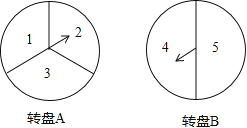
查看答案和解析>>【题目】某校初三年级(1)班要举行一场毕业联欢会.规定每个同学分别转动下图中两个可以自由转动的均匀转盘A、B(转盘A被均匀分成三等份.每份分別标上1.2,3三个钕宇.转盘B被均匀分成二等份.每份分别标上4,5两个数字).若两个转盘停止后指针所指区域的数字都为偶数(如果指针恰好指在分格线上.那么重转直到指针指向某一数字所在区域为止).则这个同学要表演唱歌节目.请求出这个同学表演唱歌节目的概率(要求用画树状图或列表方法求解)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 、
、 两个不透明的布袋,
两个不透明的布袋, 袋中有三个相同的小球,分别标有数字
袋中有三个相同的小球,分别标有数字 ,
, 和
和 ,
, 袋中有两个相同的小球,分别标有数字
袋中有两个相同的小球,分别标有数字 和
和 ,小林从
,小林从 袋中随机取出一个小球,记录标有的数字为
袋中随机取出一个小球,记录标有的数字为 ,再从
,再从 袋中随机取出一个小球,记录标有的数字为
袋中随机取出一个小球,记录标有的数字为 ,这样确定了点
,这样确定了点 的坐标
的坐标
 用画树状图或列表的形式,求点
用画树状图或列表的形式,求点 在
在 轴上的概率;
轴上的概率; 在平面直角坐标系
在平面直角坐标系 中,
中, 的半径是
的半径是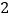 ,求过点
,求过点 能作
能作 切线的概率.
切线的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,桌面上放置了红,黄,蓝三个不同颜色的杯子,杯子口朝上,我们做蒙眼睛翻杯子(杯口朝上的翻为杯口朝下,杯口朝下的翻为杯口朝上)的游戏.

 随机翻一个杯子,求翻到黄色杯子的概率;
随机翻一个杯子,求翻到黄色杯子的概率; 随机翻一个杯子,接着从这三个杯子中再随机翻一个,请利用树状图求出此时恰好有一个杯口朝上的概率.
随机翻一个杯子,接着从这三个杯子中再随机翻一个,请利用树状图求出此时恰好有一个杯口朝上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在不透明的口袋中,有四只形状、大小、质地完全相同的小球,四只小球上分别标有数字
 ,
, ,
, ,
, 、小明先从盒子里随机取出一只小球(不放回),记下数字作为平面直角坐标系内点的横坐标;再由小华随机取出一只小球,记下数字作为平面直角坐标系内点的纵坐标.
、小明先从盒子里随机取出一只小球(不放回),记下数字作为平面直角坐标系内点的横坐标;再由小华随机取出一只小球,记下数字作为平面直角坐标系内点的纵坐标. 用列表法或画树状图,表示所有这些点的坐标;
用列表法或画树状图,表示所有这些点的坐标; 小刚为小明、小华两人设计了一个游戏:当上述
小刚为小明、小华两人设计了一个游戏:当上述 中的点在正比例函数
中的点在正比例函数 图象上方时小明获胜,否则小华获胜、你认为这个游戏公平吗?请说明理由.
图象上方时小明获胜,否则小华获胜、你认为这个游戏公平吗?请说明理由.
相关试题

