【题目】如图,直线y=kx-3与x轴、y轴分别交于点B,C, ![]() =
= ![]() .
.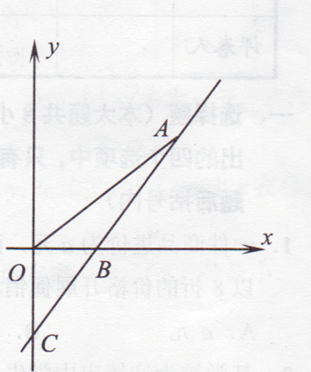
(1)求点B坐标和k值;
(2)若点A(x,y)是直线y=kx-3上在第一象限内的一个动点,当点A在运动过程中,试写出△AOB的面积S与x的函数关系式(不要求写自变量范围);并进一步求出点A的坐标为多少时,△AOB的面积为 ![]() ?
?
(3)在上述条件下,x轴上是否存在点P,使△AOP为等腰三角形?若存在,请写出满足条件的所有P点坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
(1)∵直线y=kx-3与y轴的交点为C(0,-3)
∴OC=3
∵ ![]() =
= ![]()
∴OB= ![]()
∴B点坐标为( ![]() ,0)
,0)
将B( ![]() ,0)代入y=kx-3,得
,0)代入y=kx-3,得
![]() k-1=0
k-1=0
解得k=2.
(2)
解:由(1)可知直线的解析式是y=2x-3,
S= ![]() ×OB×yA
×OB×yA
= ![]() ×
× ![]() ×(2x-3)
×(2x-3)
= ![]() x-
x- ![]()
即:三角形AOB的面积S与x的函数关系式为S= ![]() x-
x- ![]() ,
,
当S= ![]() 时,
时, ![]() x-
x- ![]() =
= ![]() ,解得x=3,则2x-3=3,即A(3,3).
,解得x=3,则2x-3=3,即A(3,3).
所以当点A的坐标为(3,3)时,△AOB的面积为 ![]() ?
?
(3)
解:存在.由(2)得A(3,3),AO=3 ![]() ,∠AOB=45°,
,∠AOB=45°,
当OP=AO=3 ![]() 时,P(3
时,P(3 ![]() ,0)或P(-3
,0)或P(-3 ![]() ,0);
,0);
当AP=OA=3 ![]() 时,∠APO=∠AOP=45°,则OP=
时,∠APO=∠AOP=45°,则OP= ![]() OA=6,P(6,0);
OA=6,P(6,0);
当OP=AP时,P(3,0).
【解析】(1)当x=0时,y=-3,即C(0,-3),由 ![]() =
= ![]() 求出B点坐标,将它代入直线y=kx-3可求出k;(2)因为点A在直线y=2x-3上,则A(x, 2x-3),由S=
求出B点坐标,将它代入直线y=kx-3可求出k;(2)因为点A在直线y=2x-3上,则A(x, 2x-3),由S= ![]() ×OB×yA , 代入相应值即可求出S关于x的函数关系式;令S=
×OB×yA , 代入相应值即可求出S关于x的函数关系式;令S= ![]() 时,求出x的值,并代入直线解析式求出A点的坐标;(3)分类讨论:当OP=AO时,当AP=OA时,当OP=AP时.结合A(3,3),AO=3
时,求出x的值,并代入直线解析式求出A点的坐标;(3)分类讨论:当OP=AO时,当AP=OA时,当OP=AP时.结合A(3,3),AO=3 ![]() ,∠AOB=45°解题即可.
,∠AOB=45°解题即可.
【考点精析】本题主要考查了一次函数的性质和一次函数的图象和性质的相关知识点,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】可以作圆,且只可以作一个圆的条件是( )
A.已知圆心
B.已知半径
C.过三个已知点
D.过不在同一直线上的三点 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽查了10名参加2016年云南省初中学业水平考试学生的体育成绩,得到的结果如表:
成绩(分)
46
47
48
49
50
人数(人)
1
2
1
2
4
下列说法正确的是( )
A.这10名同学的体育成绩的众数为50
B.这10名同学的体育成绩的中位数为48
C.这10名同学的体育成绩的方差为50
D.这10名同学的体育成绩的平均数为48 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若DH=
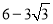 ,求EF和半径OA的长.
,求EF和半径OA的长.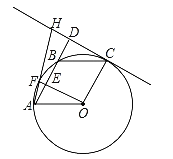
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数y=﹣
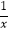 , 下列结论错误的是( )
, 下列结论错误的是( )
A.当x>0时,y随x的增大而增大
B.当x<0时,y随x的增大而增大
C.当x=1时的函数值大于x=﹣1时的函数值
D.在函数图象所在的象限内,y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于反比例函数y=
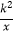 (k≠0),下列说法不正确的是( )
(k≠0),下列说法不正确的是( )
A.它的图像分布在第一、三象限
B.点(k,k)在它的图像上
C.它的图像关于原点对称
D.在每个象限内y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.坐标平面内的点与有序数对是一一对应的
B.在x轴上的点纵坐标为零
C.在y轴上的点横坐标为零
D.平面直角坐标系把平面上的点分为四部分
相关试题

