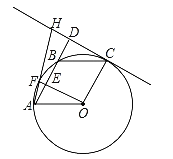
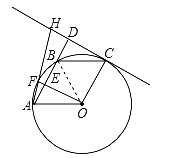
【题目】如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若DH=![]() ,求EF和半径OA的长.
,求EF和半径OA的长.
参考答案:
【答案】(1)证明见解析;(2)EF=![]() ,r=2.
,r=2.
【解析】
试题分析:(1)连接OB,根据已知条件得到△AOB是等边三角形,得到∠AOB=60°,根据圆周角定理得到∠AOF=∠BOF=30°,根据平行线的性质得到OC⊥CD,由切线的判定定理即可得到结论;
(2)根据平行线的性质得到∠DBC=∠EAO=60°,解直角三角形得到BD=![]() BC=
BC=![]() AB,推出AE=
AB,推出AE=![]() AD,根据相似三角形的性质得到
AD,根据相似三角形的性质得到![]() ,求得EF=
,求得EF=![]() ,根据直角三角形的性质即可得到结论.
,根据直角三角形的性质即可得到结论.
试题解析:(1)连接OB,∵OA=OB=OC,∵四边形OABC是平行四边形,∴AB=OC,∴△AOB是等边三角形,∴∠AOB=60°,∵∠FAD=15°,∴∠BOF=30°,∴∠AOF=∠BOF=30°,∴OF⊥AB,∵CD∥OF,∴CD⊥AD,∵AD∥OC,∴OC⊥CD,∴CD是半圆O的切线;
(2)∵BC∥OA,∴∠DBC=∠EAO=60°,∴BD=![]() BC=
BC=![]() AB,∴AE=
AB,∴AE=![]() AD,∵EF∥DH,∴△AEF∽△ADH,∴
AD,∵EF∥DH,∴△AEF∽△ADH,∴![]() ,∵DH=
,∵DH=![]() ,∴EF=
,∴EF=![]() ,∵OF=OA,∴OE=OA﹣(
,∵OF=OA,∴OE=OA﹣(![]() ),∵∠AOE=30°,∴
),∵∠AOE=30°,∴![]() =
=![]() ,解得:OA=2.
,解得:OA=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.

(1)求证:AD=BE;
(2)求∠AEB的度数;
(3)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE. ①∠AEB的度数为°;
②探索线段CM、AE、BE之间的数量关系为 . (直接写出答案,不需要说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】可以作圆,且只可以作一个圆的条件是( )
A.已知圆心
B.已知半径
C.过三个已知点
D.过不在同一直线上的三点 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽查了10名参加2016年云南省初中学业水平考试学生的体育成绩,得到的结果如表:
成绩(分)
46
47
48
49
50
人数(人)
1
2
1
2
4
下列说法正确的是( )
A.这10名同学的体育成绩的众数为50
B.这10名同学的体育成绩的中位数为48
C.这10名同学的体育成绩的方差为50
D.这10名同学的体育成绩的平均数为48 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx-3与x轴、y轴分别交于点B,C,
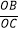 =
=  .
.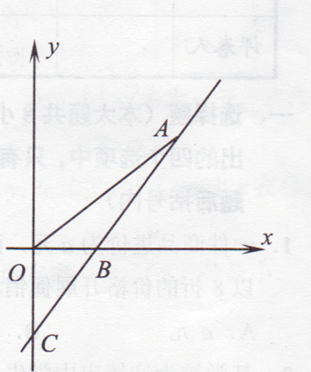
(1)求点B坐标和k值;
(2)若点A(x,y)是直线y=kx-3上在第一象限内的一个动点,当点A在运动过程中,试写出△AOB的面积S与x的函数关系式(不要求写自变量范围);并进一步求出点A的坐标为多少时,△AOB的面积为 ?
?
(3)在上述条件下,x轴上是否存在点P,使△AOP为等腰三角形?若存在,请写出满足条件的所有P点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数y=﹣
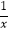 , 下列结论错误的是( )
, 下列结论错误的是( )
A.当x>0时,y随x的增大而增大
B.当x<0时,y随x的增大而增大
C.当x=1时的函数值大于x=﹣1时的函数值
D.在函数图象所在的象限内,y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于反比例函数y=
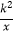 (k≠0),下列说法不正确的是( )
(k≠0),下列说法不正确的是( )
A.它的图像分布在第一、三象限
B.点(k,k)在它的图像上
C.它的图像关于原点对称
D.在每个象限内y随x的增大而增大
相关试题

