【题目】如图,四边形![]() 是正方形,
是正方形,![]() 是
是![]() 边所在直线上的点,
边所在直线上的点,![]() ,且
,且![]() 交正方形外角
交正方形外角![]() 的平分线
的平分线![]() 于点
于点![]() .
.
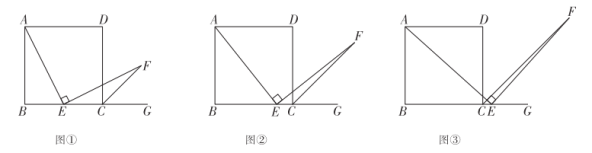
(1)当点![]() 在线段
在线段![]() 中点时(如图①),易证
中点时(如图①),易证![]() ,不需证明;
,不需证明;
(2)当点![]() 在线段
在线段![]() 上(如图②)或在线段
上(如图②)或在线段![]() 延长线上(如图③)时,(1)中的结论是否仍然成立?请写出你的猜想,并选择图②或图③的一种结论给予证明.
延长线上(如图③)时,(1)中的结论是否仍然成立?请写出你的猜想,并选择图②或图③的一种结论给予证明.
参考答案:
【答案】(1)见解析;(2)成立,理由见解析.
【解析】
(1)图①在AB上取一点M,使AM=EC,连接ME,证明△AME≌△BCF,从而可得到AE=EF;
(2)图②在AB上取一点M,使AM=EC,连接ME,证明△AME≌△BCF,从而可得到AE=EF;图③在BA的延长线上取一点N,使AN=CE,连接NE,然后证明△ANE≌△ECF,从而可得到AE=EF.
解:在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() 是外角
是外角![]() 的平分线,
的平分线,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
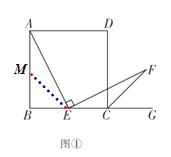
(2)图②结论:![]() .图③结论:
.图③结论:![]() .
.
图②证明:如图②,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() 是外角
是外角![]() 的平分线,
的平分线,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.

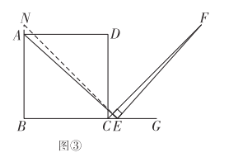
图③证明:如图③,在![]() 的延长线上取一点
的延长线上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
∴![]() .
.
∴![]() .
.
∵四边形![]() 是正方形,
是正方形,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李国庆长假期间的某天下午的营运全是在南北走向的城区市心路上进行的,如果规定向南行驶为正,他这天下午行车的里程(单位:千米)如下:
+8,﹣6,﹣5,+10,﹣5,+3,﹣2,+6,+2,﹣5
(1)小李下午出发地记为0,他将最后一名乘客送抵目的地时,小李距下午出发地有多远?
(2)如果汽车耗油量为0.4升/千米,油价每升5.80元,那么这天下午汽车共需花费油价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量保持不变,容器内水量
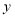 (单位:
(单位: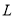 )与时间
)与时间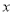 (单位:
(单位: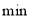 )的部分函数图象如图所示,请结合图象信息解答下列问题:
)的部分函数图象如图所示,请结合图象信息解答下列问题: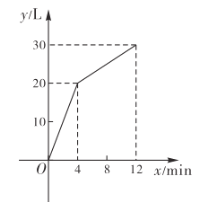
(1)求出水管的出水速度;
(2)求
 时容器内的水量;
时容器内的水量;(3)从关闭进水管起多少分钟时,该容器内的水恰好放完?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

-
科目: 来源: 题型:
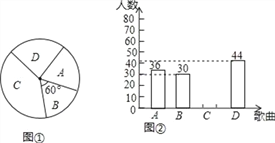
查看答案和解析>>【题目】为庆祝建军90周年,某校计划在五月份举行“唱响军歌”歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱歌曲.为此提供代号为A,B,C,D四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制如下两幅不完整的统计图.请根据图①,图②所提供的信息,
解答下列问题:
(1)本次抽样调查中,选择曲目代号为A的学生占抽样总数的百分比为 ;
(2)请将图②补充完整;
(3)若该校共有1260名学生,根据抽样调查的结果估计全校共有多少学生选择喜欢人数最多的歌曲?(要有解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数
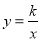 (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.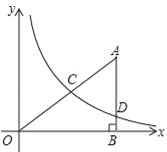
(1)求反比例函数
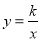 的解析式;
的解析式;(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O为直线AD上一点,OB是∠AOC内部一条射线且满足∠AOB与∠AOC互补,OM、ON分别为∠AOC、∠AOB的平分线.
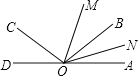
(1)∠COD与∠AOB相等吗?请说明理由;
(2)若∠AOB=30°,试求∠AOM与∠MON的度数;
(3)若∠MON=55°,试求∠AOC的度数.
相关试题

