【题目】方程也可以用来解决一些几何问题，如图，P为△ABC内一点，连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F，则把△ABC分成六个小三角形，其中四个小三角形面积已在图上标明，设△BPD的面积为，△CPE的面积为，

（1） ； （填数字）；

（2）求的值．

参考答案：

【答案】（1），；（2）

【解析】分析：（1）根据等高不等底的三角形的面积的比等于底边的比，即可求得底边之间的关系；

（2）根据S△AFC：S△BFC＝AF：BF和S△BPC：S△EPC＝BP：EP关系列，列出关于x、y的二元一次方程组，解方程组即可;

详解：

（1）∵S△BFP==56, S△AFP==84,

∴ BF:AF=56:84，即AF＝BF，

同理可证：BP：PE＝（56+84）：70＝2：1,即BP=2PE.

（2）∵S△AFC：S△BFC＝AF：BF, S△BPC：S△EPC＝BP：EP

∴

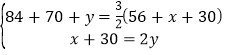
解得

关闭