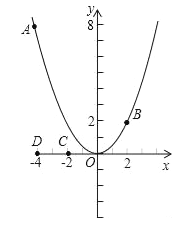
【题目】如图,已知点A(﹣4,8)和点B(2,n)在抛物线y=ax2上.
(1)求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2)平移抛物线y=ax2,记平移后点A的对应点为A′,点B的对应点为B′,点C(﹣2,0)和点D(﹣4,0)是x轴上的两个定点.
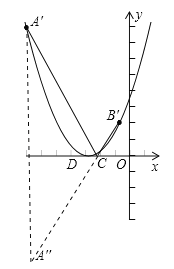
①当抛物线向左平移到某个位置时,A′C+CB′最短,求此时抛物线的函数解析式;
②当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
参考答案:
【答案】(1)a= ![]() ,P的坐标为(2,﹣2),Q的坐标是(
,P的坐标为(2,﹣2),Q的坐标是(![]() ,0);(2)①
,0);(2)①![]() ;②存在,
;②存在,![]() .
.
【解析】试题分析:(1)把(﹣4,8)代入y=ax2可求得a的值,把x=2代入所求的抛物线解析式,可得n的值,那么P的坐标为2,纵坐标为﹣n,求得AP与x轴的交点即为Q的坐标;
(2)A′C+CB′最短,说明抛物线向左平移了线段CQ的距离,用顶点式设出相应的函数解析式,把新顶点坐标代入即可;
(3)左右平移时,使A′D+DB′′最短即可,那么作出点A′关于x轴对称点的坐标为A′′,得到直线A′′B′′的解析式,让y=0,求得相应的点的坐标;进而得到抛物线顶点平移的规律,用顶点式设出相应的函数解析式,把新顶点坐标代入即可.
试题解析:解:(1)将点A(﹣4,8)的坐标代入y=ax2,解得a=![]() ;
;
将点B(2,n)的坐标代入y=![]() x2,求得点B的坐标为(2,2),则点B关于x轴对称点P的坐标为(2,﹣2),设直线AP的解析式为y=kx+b,
x2,求得点B的坐标为(2,2),则点B关于x轴对称点P的坐标为(2,﹣2),设直线AP的解析式为y=kx+b,![]() ,解得:
,解得: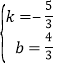 ,∴直线AP的解析式是y=﹣
,∴直线AP的解析式是y=﹣![]() x+
x+![]() ,令y=0,得:x=
,令y=0,得:x=![]() .
.
即所求点Q的坐标是(![]() ,0);
,0);
(2)①CQ=|﹣2﹣![]() |=
|=![]() ,
,
故将抛物线y=![]() x2向左平移
x2向左平移![]() 个单位时,A′C+CB′最短,
个单位时,A′C+CB′最短,
此时抛物线的函数解析式为y=![]() (x+
(x+![]() )2;
)2;
②左右平移抛物线y=![]() x2.∵线段A′B′和CD的长是定值,∴要使四边形A′B′CD的周长最短,只要使A′D+CB′最短;
x2.∵线段A′B′和CD的长是定值,∴要使四边形A′B′CD的周长最短,只要使A′D+CB′最短;
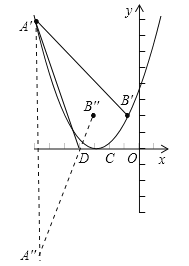
第一种情况:如果将抛物线向右平移,显然有A′D+CB′>AD+CB,∴不存在某个位置,使四边形A′B′CD的周长最短;
第二种情况:设抛物线向左平移了b个单位,则点A′和点B′的坐标分别为A′(﹣4﹣b,8)和B′(2﹣b,2).∵CD=2,∴将点B′向左平移2个单位得B′′(﹣b,2),要使A′D+CB′最短,只要使A′D+DB′′最短,点A′关于x轴对称点的坐标为A′′(﹣4﹣b,﹣8).∵直线A′′B′′的解析式为y=![]() x+
x+![]() b+2.要使A′D+DB′′最短,点D应在直线A′′B′′上,将点D(﹣4,0)代入直线A′′B′′的解析式,解得:b=
b+2.要使A′D+DB′′最短,点D应在直线A′′B′′上,将点D(﹣4,0)代入直线A′′B′′的解析式,解得:b=![]() ,∴将抛物线向左平移时,存在某个位置,使四边形A′B′CD的周长最短,此时抛物线的函数解析式为y=
,∴将抛物线向左平移时,存在某个位置,使四边形A′B′CD的周长最短,此时抛物线的函数解析式为y=![]() (x+
(x+![]() )2.
)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,A(-1,1),B(-4,2),C(-3,4).
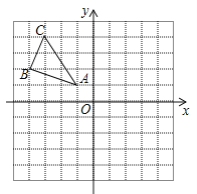
(1)在网格中画出△ABC向右平移5个单位后的图形△A1B1C1;
(2)在网格中画出△ABC关于原点O成中心对称后的图形△A2B2C2;
(3)请直接写出点B2、C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】俄罗斯足球世界杯点燃了同学们对足球运动的热情,某学校划购买甲、乙两种品牌的足球供学生使用.已知用1000 元购买甲种足球的数量和用1600元购买乙种足球的数量相同,甲种足球的单价比乙种足球的单价少30元.
(1)求甲、乙两种品牌的足球的单价各是多少元?
(2)学枝准备一次性购买甲、乙两种品牌的足球共25个,但总费用不超过1610元,那么这所学校最多购买多少个乙种品牌的足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在图1至图3中,直线MN与线段AB相交于点O,∠1=∠2=45°.
(1)如图1,若AO=OB,请写出AO与BD的数量关系和位置关系;
(2)将图1中的MN绕点O顺时针旋转得到图2,其中AO=OB.求证:AC=BD,AC⊥BD;
(3)将图2中的OB拉长为AO的k倍得到图3,求
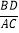 的值.
的值.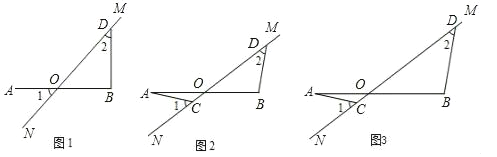
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AB的中点,连接DE、CE.
(1)求证:△ADE≌△BCE;
(2)若AB=6,AD=4,求△CDE的周长.

-
科目: 来源: 题型:
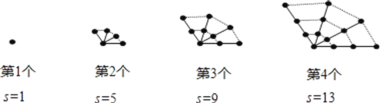
查看答案和解析>>【题目】观察图中给出的四个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第10个点阵中的点的个数s为( ).
A.
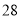 B.
B.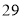 C.
C.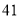 D.
D.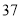
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
相关试题

