【题目】2019年双“11”期间,哈市各大商场掀起购物狂潮,现有甲、乙、丙三个商场开展的促销活动如下表所示:

根据以上活动信息,解决以下问题:
(1)三个商场都同时出售一套(一件上衣和一条裤子为一套)同厂家、同面料、同款式的服装,其中上衣标价都为290元,裤子标价都为270元.试计算三个商场分别按照促销活动销售出这一套服装的售价是多少元?
(2)赵先生发现在甲、乙商场同时出售一件标价380元的上衣和一条标价300多元的裤子,最后付款额也一样,请问这条裤子的标价是多少元?
(3)如果某种品牌的巴西大豆在三所商场的标价都是5元/![]() ,请探究:是否存在分别在三所商场付同样多的一百多元,并且都能够够买同样重量同品牌的该大豆?如果存在请直接说明在乙商场该购买大豆的方案(并指出在三个商场购买大豆的重量是多少
,请探究:是否存在分别在三所商场付同样多的一百多元,并且都能够够买同样重量同品牌的该大豆?如果存在请直接说明在乙商场该购买大豆的方案(并指出在三个商场购买大豆的重量是多少![]() ,支付的费用是多少元);如果不存在请直接回答“不存在”.
,支付的费用是多少元);如果不存在请直接回答“不存在”.
参考答案:
【答案】(1)甲:336元;乙:360元;丙:310元;(2)370元;(3)存在,先购买30kg大豆付150元,再用100元购物券在乙商城购买20kg大豆,总共付150元,购买50kg大豆
【解析】
(1)根据题意和促销方式分别求出结论即可;
(2)设这条裤子的标价为x元,根据题意列出方程即可求出结论;
(3)设在乙商场先购买ykg大豆,需付一百多元,再用100元的购物卷再在乙商场购买100÷5=20kg大豆,根据在甲、乙两商场付同样多的一百多元,并且都能够够买同样重量同品牌的该大豆列出方程,即可求出y,再求出在丙商场所需付款即可得出结论.
解:(1)选甲商城需付费用为(290+270)×0.6=336(元)
选乙商城需付费用为290+(270﹣200)=360(元)
选丙商城需付费用为290+270﹣5×50=310(元)
答:选甲商城需付费用为336元;选乙商城需付费用为360元;选丙商城需付费用为310元.
(2)设这条裤子的标价为x元,根据题意得:
(380+x)×0.6=380+x﹣100×3
解得:x=370
答:这条裤子的标价为370元.
(3)解:存在
设在乙商场先购买ykg大豆,需付一百多元,再用100元的购物卷再在乙商场购买100÷5=20kg大豆
由题意可得5(y+20)×0.6=5y
解得:y=30
此时,在甲商场和乙商场共购买30+20=50kg都需付款30×5=150(元)
在丙商场购买50kg需5×50-2×50=150(元)
∴存在分别在三所商场付同样多的一百多元,并且都能够够买同样重量同品牌的该大豆,
在乙商场购买方案为:先购买30![]() 大豆付150元;再用100元的购物卷再在乙商场购买20kg大豆,总共付了150元,购买了50kg大豆.
大豆付150元;再用100元的购物卷再在乙商场购买20kg大豆,总共付了150元,购买了50kg大豆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1△ABC为等边三角形,点D为AB边上的一点,∠DCE=30°,∠DCF=60°且CF=CD
(1)求∠EAF的度数;
(2)DE与EF相等吗?请说明理由

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.不可能事件发生的概率为0
B.随机事件发生的概率为
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于( )

A.50°
B.60°
C.70°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为5,P为⊙O上一点,P(4,3),PC、PD为⊙O的弦,分别交y轴正半轴于E、F,且PE=PF,连CD,设直线CD为y=kx+b,则k= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在数轴上点A,点B对应的数分别是6,﹣6,∠DCE=90°(点C与点O重合,点D在数轴的正半轴上)
(1)如图1,若CF平分∠ACE,则∠AOF= 度;点A与点B的距离=
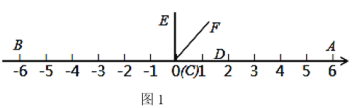
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.

①当t=1时,α= ;点B与点C的距离=
②猜想∠BCE和α的数量关系,并说明理由;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0
 t
t 3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0
3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0 t
t 3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,求t的值.
3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,求t的值.
相关试题

