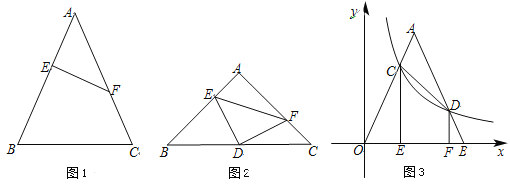
【题目】定义:如图1,等腰△ABC中,点E,F分别在腰AB,AC上,连结EF,若AE=CF,则称EF为该等腰三角形的逆等线.
(1)如图1,EF是等腰△ABC的逆等线,若EF⊥AB,AB=AC=5,AE =2,求逆等线EF的长;
(2)如图2,若等腰直角△DEF的直角顶点D恰好为等腰直角△ABC底边BC上的中点,且点E,F分别在AB,AC上,求证:EF为等腰△ABC的逆等线;
(3)如图3,等腰△AOB的顶点O与原点重合,底边OB在x轴上,反比例函数y= ![]() (x>0)的图象交△OAB于点C,D,若CD恰为△AOB的逆等线,过点C,D分别作CE⊥x轴,DF⊥x轴,已知OE=2,求OF的长.
(x>0)的图象交△OAB于点C,D,若CD恰为△AOB的逆等线,过点C,D分别作CE⊥x轴,DF⊥x轴,已知OE=2,求OF的长.
参考答案:
【答案】(1)逆等线EF的长为![]() ;
;
(2)EF为等腰△ABC的逆等线;
(3)OF=2![]() +2
+2
【解析】试题分析:(1)、根据逆等线的定义得出CF=AE=2,AF=3,根据勾股定理得出EF的长度;(2)、连接AD,根据题意证明出△EDA和△FDC全等,从而得出AE=CF,得到逆等线;(3)、设OF=x,作AG⊥OB,CH⊥AG,根据逆等线的性质得出△ACH和△DBF全等,从而得出EG=x-4,根据△ACH和△COE相似得出x的值,从而得出x的值,即OF的长度.
试题解析:(1)∵EF是等腰△ABC的逆等线
∴CF =AE=2,又AB=AC=5 ∴AF=3 ∵EF⊥AB ∴EF=![]() =
=![]()
(2)连结AD,在等腰Rt△ABC中,点D为底边上中点 ∴AD=CD且∠ADC=90°
又∵DE=DF且∠EDF=90° ∴∠EDA=90°-∠ADF=∠FDC
∴△EDA≌△FDC ∴AE=CF ∴EF为等腰△ABC的逆等线
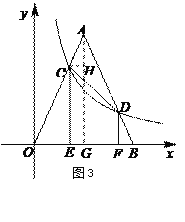
(3)如图3,设OF=x,则DF=![]() 作AG⊥OB,CH⊥AG
作AG⊥OB,CH⊥AG
∵CD为△AOB的逆等线 ∴AC=BD,又∠ACH=∠AOB=∠DBF
且∠AHC=∠AGO=∠DFB ∴△ACH≌△DBF 则EG=CH=BF,AH=DF
又AO=AB,且AG⊥OB ∴OG=BG ∴GF=BG-BF=OG-EG=OE
所以EG=x-2-2=x-4 ∵△ACH∽△COE ∴![]() =
=![]() 即
即![]() =
=![]()
化简得x2-4x-4=0 所以x=2![]() +2 即OF=2
+2 即OF=2![]() +2
+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校校门口有一个长为9m的长条形(长方形)电子显示屏,学校的有关活动都会在“电子显示屏”播出,由于各次活动的名称不同,字数也就不等,为了制作及显示时方便美观,负责播出的老师对有关数据作出了如下规定:若字数在8个以下,边空:字宽:字距=2:4:1;若字数在8个以上(含8个),边空:字宽:字距=2:3:1,如图所录:

(1)某次活动的字数为9个,求字距是多少?
(2)如果某次活动的字宽为36cm,问字数是多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的一个外角等于30°,则这个正多边形的边数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由两个正方形组成的长方形花坛ABCD,小明从顶点A沿着花坛间小路直到走到长边中点O,再从中点O走到正方形OCDF的中心O1 , 再从中心O1走到正方形O1GFH的中心O2 , 又从中心O2走到正方形O2IHJ的中心O3 , 再从中心O3走2走到正方形O3KJP的中心O4 , 一共走了31
 m,则长方形花坛ABCD的周长是 .
m,则长方形花坛ABCD的周长是 . 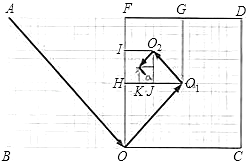
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组﹣1<x<4的整数解有_________个.
-
科目: 来源: 题型:
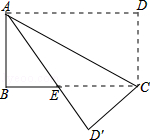
查看答案和解析>>【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式由左边到右边的变形中,属于因式分解的是( )
A.x2﹣2x+2=x(x﹣2)+2
B.(x+y)(x﹣y)=x2﹣y2
C.(2a﹣b)2=4a2﹣4ab+b2
D.x2+4x+4=(x+2)2
相关试题

