搜索
【题目】如图，小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏，他将纸片沿EF折叠后，D，C两点分别落在点D′，C′的位置，∠DEF＝∠D′EF，并利用量角器量得∠EFB＝66°，则∠AED′的度数为( )
A. 66°B. 132°C. 48°D. 38°
参考答案：
【答案】C
【解析】
先根据平角的定义求出∠EFC，根据平行线的性质求出∠DEF，根据折叠求出∠D′EF，即可求出答案．
解：∵∠EFB=66°，
∴∠EFC=180°-66°=114°，
∵四边形ABCD是长方形，
∴AD∥BC，
∴∠DEF=180°-∠EFC=180°-114°=66°，
∵沿EF折叠D和D′重合，
∴∠D′EF=∠DEF=66°，
∴∠AED′=180°-66°-66°=48°．
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学开展“阳光体育一小时”活动，根据学校实际情况，决定开设①踢毽子；②篮球；③跳绳；④乒乓球四种运动项目．为了解学生最喜欢哪一种运动项目，随机抽取了一部分学生进行调查，并将调查结果绘制成如下不完整的两个统计图，依据图中信息，得出下列结论中正确的是( )
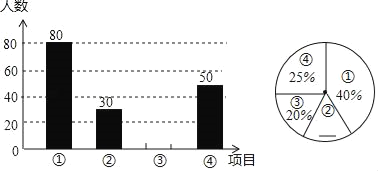
A. 本次共调查300名学生
B. 扇形统计图中，喜欢篮球项目的学生部分所对应的扇形圆心角大小为45°
C. 喜欢跳绳项日的学生人数为60人
D. 喜欢篮球项目的学生人数为30人
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是 ．
-
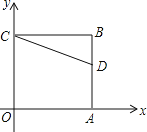
科目： 来源： 题型：
查看答案和解析>>【题目】图①是一个长为
、宽为
的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形．
（1）图②中的阴影部分的面积为______；
（2）观察图②请你写出三个代数式
、
、
之间的等量关系是：__________；（3）实际上有许多代数恒等式可以用图形的面积来表示．如图③，它表示了___________．
（4）请你用图③提供的若干块长方形和正方形硬纸片图形，用拼长方形的方法，把下列二次三项式进行因式分解：
．要求：在图④的框中画出图形；写出分解的因式． -
科目： 来源： 题型：
查看答案和解析>>【题目】若两条抛物线的顶点相同，则称它们为“友好抛物线”，抛物线C1：y1=﹣2x2+4x+2与C2：u2=﹣x2+mx+n为“友好抛物线”．
（1）求抛物线C2的解析式．
（2）点A是抛物线C2上在第一象限的动点，过A作AQ⊥x轴，Q为垂足，求AQ+OQ的最大值．
（3）设抛物线C2的顶点为C，点B的坐标为（﹣1，4），问在C2的对称轴上是否存在点M，使线段MB绕点M逆时针旋转90°得到线段MB′，且点B′恰好落在抛物线C2上？若存在求出点M的坐标，不存在说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：
对于二次三项式
可以直接用公式法分解为
的形式，但对于二次三项式
，就不能直接用公式法了，我们可以在二次三项式中先加上一项
，使其成为完全平方式，再减去这项，使整个式子的值不变.于是有=＋－=
=
．像上面这样把二次三项式分解因式的方法叫做添(拆）项法.
（1）请用上述方法把x2－4x＋3分解因式.
(2)多项式x2＋2x＋2有最小值吗？如果有，那么当它有最小值时x的值是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若AC=6，BC=8，OA=2，求线段DE的长．
相关试题
