【题目】 如图,已知等腰直角三角形![]() ,点
,点![]() 是斜边
是斜边![]() 上一点(不与
上一点(不与![]() 重合),
重合),![]() 是
是![]() 的外接圆⊙
的外接圆⊙![]() 的直径.
的直径.

(1)求证:![]() 是等腰直角三角形;
是等腰直角三角形;
(2)若⊙![]() 的直径为2,求
的直径为2,求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析(2)4
【解析】
试题分析:(1)根据等腰直角三角形性质得出∠C=∠ABC=∠PEA=45°,再由PE是⊙O的直径,得出∠PAE=90°,∠PEA=∠APE=45°,从而得证.
(2)根据题意可知,AC=AB,AP=AE,再证△CPA≌△BAE,得出CP=BE,依勾股定理即可得证.
试题解析:(1)证明:∵△ABC是等腰直角三角形,
∴∠C=∠ABC=45°,
∴∠PEA=∠ABC=45°
又∵PE是⊙O的直径,
∴∠PAE=90°,
∴∠PEA=∠APE=45°,
∴ △APE是等腰直角三角形.
(2)∵△ABC是等腰直角三角形,
∴AC=AB,
同理AP=AE,
又∵∠CAB=∠PAE=90°,
∴∠CAP=∠BAE,
∴△CPA≌△BAE,
∴CP=BE,
在Rt△BPE中,∠PBE=90°,PE=2,
∴PB2+BE2=PE2,
∴CP2+PB2=PE2=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015深圳国际马拉松赛预报名11月2日上午9时启动,开放报名一小时内官网访问量就超过23万,23万用科学记数法表示是( )
A.2.3×105
B.2.3×104
C.0.23×102
D.0.23×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个十边形的每一个外角都相等,那么它的一个内角的度数为_____________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,有两个全等的直角三角形△ABC和△EDF,∠ACB=∠F=90°,∠A=∠E=30°,点D在边AB上,且AD=BD=CD.△EDF绕着点D旋转,边DE,DF分别交边AC于点M,K.

(1)如图2、图3,当∠CDF=0°或60°时,AM+CKMK(填“>”,“<”或“=”),你的依据是;

(2)如图4,当∠CDF=30°时,AM+CKMK(填“>”或“<”);
(3)猜想:如图1,当0°<∠CDF<60°时,AM+CKMK,试证明你的猜想.. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块三角形玻璃损坏后,只剩下如图所示的残片,对图中的哪些数据测量后就可到建材部门割取符合规格的三角形玻璃( )
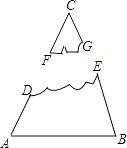
A.∠A,∠B,∠C
B.∠A,线段AB,∠B
C.∠A,∠C,线段AB
D.∠B,∠C,线段AD -
科目: 来源: 题型:
查看答案和解析>>【题目】 在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程
 ,操作步骤是:
,操作步骤是:第一步:根据方程的系数特征,确定一对固定点
 ;
;第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点
 ,另一条直角边恒过点
,另一条直角边恒过点 ;
;第三步:在移动过程中,当三角板的直角顶点落在
 轴上点
轴上点 处时,点
处时,点 的横坐标
的横坐标 即为该方程的一个实数根(如图1);
即为该方程的一个实数根(如图1);第四步:调整三角板直角顶点的位置,当它落在
 轴上另—点
轴上另—点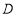 处时,点
处时,点 的横坐标
的横坐标 即为该方程的另一个实数根.
即为该方程的另一个实数根.
(1)在图2中,按照“第四步”的操作方法作出点
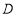 (请保留作出点
(请保留作出点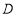 时直角三角板两条直角边的痕迹);
时直角三角板两条直角边的痕迹); (2)结合图1,请证明“第三步”操作得到的
 就是方程
就是方程 的一个实数根;
的一个实数根;(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程

 的实数根,请你直接写出一对固定点的坐标;
的实数根,请你直接写出一对固定点的坐标;(4)实际上,(3)中的固定点有无数对,一般地,当
 与
与 之间满足怎样的关系时,点
之间满足怎样的关系时,点 就是符合要求的—对固定点?
就是符合要求的—对固定点?
相关试题

