【题目】如图,下列条件中,不能证明△ABD≌△ACD的是( )

A. AB=AC,BD=CD B. ∠B=∠C,BD=CD
C. ∠B=∠C,∠BAD=∠CAD D. ∠ADB=∠ADC,DB=DC
参考答案:
【答案】B
【解析】
根据全等三角形的判定即可解题。
解:A、BD=DC,AB=AC,再加公共边AD=AD可利用SSS定理进行判定,故此选项不合题意;
B、∠B=∠C,BD=CD,再加公共边AD=AD不能判定△ABD≌△ACD,故此选项符合题意;
C、∠B=∠C,∠BAD=∠CAD再加公共边AD=AD可利用AAS定理进行判定,故此选项不合题意;
D、∠ADB=∠ADC,BD=DC再加公共边AD=AD可利用SAS定理进行判定,故此选项不合题意;
故选B
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在工程招标时,接到甲、乙两个工程队的投标书.每施工一天,需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,形成下列三种施工方案:
方案①:甲队单独完成此项工程刚好如期完工;
方案②:乙队单独完成此项工程要比规定工期多用5天;
方案③:若甲、乙两队合作4天,剩下的工程由乙队独做也正好如期完工;
(1)求甲、乙两队单独完成此项工程各需多少天?
(2)如果工程不能如期完工,公司每天将损失3000元,如果你是公司经理,你觉得哪一种施工方案划算,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的符号表示下面的关系:
(1)a的一半比a与3的差小. (2)x的
 与5的差小于1.
与5的差小于1.(3)x与6的和大于-7. (4)8与y的2倍的和是正数.
(5)a的3倍与7的差是负数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一堆有红、白两种颜色的球若干个,已知白球的个数比红球少,但白球的2倍比红球多.若把每一个白球都记作“2”,每一个红球都记作“3”,则总数为“60”,那么这两种球各有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,下列条件中,不能说明AB⊥CD的是( )

A. ∠AOD=90°
B. ∠AOC=∠BOC
C. ∠BOC+∠BOD=180°
D. ∠AOC+∠BOD=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为________,∠BOE的补角为________;
(2)若∠AOC=75°,且∠BOE∶∠EOD=1∶4,求∠AOE的度数.
-
科目: 来源: 题型:
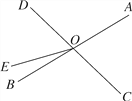
查看答案和解析>>【题目】如图,直线AB,CD,EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.

相关试题

