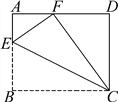
【题目】如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为___.
参考答案:
【答案】![]()
【解析】试题分析:由四边形ABCD是矩形,可得:∠A=∠B=∠D=90°,CD=AB=4,AD=BC=5,由折叠的性质可得:∠EFC=∠B=90°,CF=BC=5,由同角的余角相等,即可得∠DCF=∠AFE,然后在Rt△DCF中,即可求得答案:∵四边形ABCD是矩形,
∴∠A=∠B=∠D=90°,CD=AB=4,AD=BC=5,
由题意得:∠EFC=∠B=90°,CF=BC=5,
∴∠AFE+∠DFC=90°,∠DFC+∠FCD=90°,
∴∠DCF=∠AFE,
∵在Rt△DCF中,CF=5,CD=4,
∴DF=3,
∴tan∠AFE=tan∠DCF=![]() .
.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两根旗杆间相距12m,某人从点B沿BA走向点A,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,则这个人运动到点M所用时间是_______________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则( )

A.点B到AO的距离为sin54°
B.点B到AO的距离为tan36°
C.点A到OC的距离为sin36°sin54°
D.点A到OC的距离为cos36°sin54°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立的是( )

A. DA=DEB. BD=CEC. ∠EAC=90°D. ∠ABC=2∠E
-
科目: 来源: 题型:
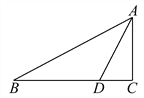
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AC=6,CD=3,∠ADC=α.
(1)试写出α的正弦、余弦、正切这三个函数值;
(2)若∠B与∠ADC互余,求BD及AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.

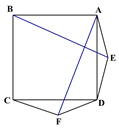

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

相关试题

