【题目】已知在关于x的分式方程![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当方程②有两个整数根x1、x2,k为整数,且k=m+2,n=1时,求方程②的整数根;
(3)当方程②有两个实数根x1、x2,满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.
参考答案:
【答案】(1) k≥﹣1且k≠1且k≠2;(2) x1=0,x2=3;(3)成立
【解析】试题分析:(1)先解出分式方程①的解,根据分式的意义和方程①的根为非负数得出k的取值;(2)先把k=m+2,n=1代入方程②化简,由方程②有两个整数实根得△是完全平方数,列等式得出关于m的等式,由根与系数的关系和两个整数根x1、x2得出m=1和﹣1,分别代入方程后解出即可;(3)根据(1)中k的取值和k为负整数得出k=﹣1,化简已知所给的等式,并将两根和与积代入计算求出m的值,做出判断.
试题解析:(1)∵关于x的分式方程![]() 的根为非负数, ∴x≥0且x≠1,
的根为非负数, ∴x≥0且x≠1,
又∵x=![]() ≥0,且
≥0,且![]() ≠1, ∴解得k≥﹣1且k≠1,
≠1, ∴解得k≥﹣1且k≠1,
又∵一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0中2﹣k≠0, ∴k≠2,
综上可得:k≥﹣1且k≠1且k≠2;
(2)∵一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0有两个整数根x1、x2,且k=m+2,n=1时,
∴把k=m+2,n=1代入原方程得:﹣mx2+3mx+(1﹣m)=0,即:mx2﹣3mx+m﹣1=0,
∴△≥0,即△=(﹣3m)2﹣4m(m﹣1),且m≠0, ∴△=9m2﹣4m(m﹣1)=m(5m+4),
∵x1、x2是整数,k、m都是整数, ∵x1+x2=3,x1x2=![]() =1﹣
=1﹣![]() , ∴1﹣
, ∴1﹣![]() 为整数,
为整数,
∴m=1或﹣1, ∴把m=1代入方程mx2﹣3mx+m﹣1=0得:x2﹣3x+1﹣1=0, x2﹣3x=0,
x(x﹣3)=0, x1=0,x2=3;
把m=﹣1代入方程mx2﹣3mx+m﹣1=0得:﹣x2+3x﹣2=0, x2﹣3x+2=0, (x﹣1)(x﹣2)=0, x1=1,x2=2;
(3)|m|≤2不成立,理由是:
由(1)知:k≥﹣1且k≠1且k≠2, ∵k是负整数, ∴k=﹣1,
(2﹣k)x2+3mx+(3﹣k)n=0且方程有两个实数根x1、x2,
∴x1+x2=﹣![]() =
=![]() =﹣m,x1x2=
=﹣m,x1x2=![]() =
=![]() ,
,
x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k), x12﹣x1
x12+x22═x1x2+k2, (x1+x2)2﹣2x1x2﹣x1x2=k2, (x1+x2)2﹣3x1x2=k2,
(﹣m)2﹣3×![]() =(﹣1)2, m2﹣4=1, m2=5, m=±
=(﹣1)2, m2﹣4=1, m2=5, m=±![]() , ∴|m|≤2不成立.
, ∴|m|≤2不成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若⊙O的半径为4cm,点A到圆心O的距离为3cm,那么点A与⊙O的位置关系是( )
A. 点A在圆内 B. 点A在圆上 C. 点A在圆外 D. 不能确定
-
科目: 来源: 题型:
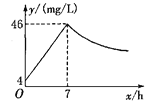
查看答案和解析>>【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度呈直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降,如图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34 mg/L时,井下3 km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4 mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
-
科目: 来源: 题型:
查看答案和解析>>【题目】两人各抛一枚硬币,则下面说法正确的是( )
A. 每次抛出后出现正面或反面是一样的
B. 抛掷同样的次数,则出现正、反面的频数一样多
C. 在相同条件下,即使抛掷的次数很多,出现正、反面的频数也不一定相同
D. 当抛掷次数很多时,出现正、反面的次数就相同了
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=6,AC=8,BC=10,D是△ABC内部或BC边上的一个动点(与B、C不重合),以D为顶点作△DEF,使△DEF∽△ABC(相似比k>1),EF∥BC.
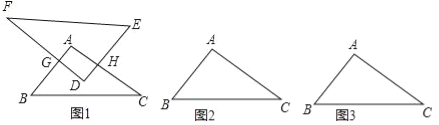
(1)求∠D的度数;
(2)若两三角形重叠部分的形状始终是四边形AGDH.
①如图1,连接GH、AD,当GH⊥AD时,请判断四边形AGDH的形状,并证明;
②当四边形AGDH的面积最大时,过A作AP⊥EF于P,且AP=AD,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是( )
A. 100(1+x)2=81 B. 100(1-x)2=81
C. 100(1-x%)2=81 D. 100x2=81
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕边AC所在直线旋转一周得到圆锥,则该圆锥的侧面积是( )
A. 25π B. 65π C. 90π D. 130π
相关试题

