【题目】如图,在△ABC中,∠ACB=120°,BC=2AC.
(1)利用尺规作等腰△DBC,使点D、A在直线BC的同侧,且DB=BC,∠DBC=∠ACB(保留作图痕迹,不写画法);
(2)设(1)中所作的△DBC的边DC交AB于E点,求证:DE=3CE.

参考答案:
【答案】(1)作图见解析;(2)证明见解析.
【解析】试题分析:(1)按照题意画出相应的图形,如图所示;
(2)利用等腰三角形BCD的性质、△DBC的内角和定理和图形中的角与角间的数量关系来求∠ACE的度数;过点B作BM⊥DC于点M.由全等三角形△BME与△ACE的对应边相等推知ME=CE=![]() MC.然后根据等腰三角形“三合一”的性质证得DM=MC,最后由等量代换证得结论.
MC.然后根据等腰三角形“三合一”的性质证得DM=MC,最后由等量代换证得结论.
试题解析:(1)如图所示,根据题意画出图形;
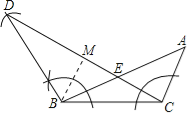
(2)∵BD=BC(已知),
∴∠D=∠BCD(等边对等角).
又∵∠DBC=120°,∠D+∠BCD+∠DBC=180°(三角形内角和定理),
∴∠D=∠BCD=30°.
∵∠ACB=120°,∠ACB=∠ACE+∠BCD,
∴∠ACE=90°,
过点B作BM⊥DC于点M,
在Rt△BMC中,由∠BCD=30°,得BM=![]() BC,
BC,
∵BC=2AC,
∴AC=![]() BC,
BC,
∴BM=AC,
在△BME与△ACE中,
∵ ,
,
∴△BME≌△ACE(AAS),
∴ME=CE=![]() MC.
MC.
∵BD=BC,BM⊥DC,
∴DM=MC,
∴ME=CE=![]() DM,
DM,
∴DE=3CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】市政府建设一项水利工程,某运输公司承担运送总量为106m3的土石方任务,该公司有甲、乙两种型号的卡车共100辆,甲型车平均每天可以运送土石方80m3,乙型车平均每天可以运送土石方120m3,计划100天完成运输任务.
(1)该公司甲、乙两种型号的卡车各有多少台?
(2)如果该公司用原有的100辆卡车工作了40天后,由于工程进度的需要,剩下的所有运输任务必须在50天内完成,在甲型卡车数量不变情况下,公司至少应增加多少辆乙型卡车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列表述中,不能表示代数式“4a”的意义的是( )
A.4的a倍B.a的4倍C.4个a相加D.4个a相乘
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2﹣1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在五边形ABCDE中,AB=AC=AD=AE, 且AB∥ED,∠AED=70°,则∠DCB=( )
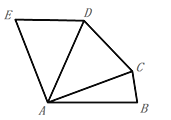
A. 70° B. 165° C. 155° D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的周长为26cm,这个长方形的长减少1cm,宽增加2cm,就可成为一个正方形,设长方形的长为xcm,则可列方程( )
A.x﹣1=(26﹣x)+2
B.x﹣1=(13﹣x)+2
C.x+1=(26﹣x)﹣2
D.x+1=(13﹣x)﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】﹣10+8÷(﹣2)2﹣(﹣2)3×(﹣3)
相关试题

