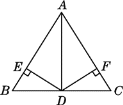
【题目】如图,AB=AC,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则下列四个结论中:①DE=DF;②AD上任意一点到AB,AC的距离相等;③∠BDE=∠CDF;④BD=CD且AD⊥BC,其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】D
【解析】
由题意知,△ABC是等腰三角形,由三线合一的性质知,点D是BC的中点,AD⊥BC,可得④正确;根据角平分线的性质可得①②正确;再由∠DEB=∠DFC=90°,∠B=∠C,根据三角形内角和定理可得③正确;故可得到4个结论均正确.
解:∵AB=AC,
∴△ABC是等腰三角形,∠B=∠C.
∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴AD⊥BC,BD=CD,DE=DF,AD上任意一点到AB、AC的距离相等,故①②④正确;
∵DE⊥AB于E,DF⊥AC,
∴∠DEB=∠DFC=90°.
∵∠DEB=∠DFC=90°,∠B=∠C,
∴∠BDE=∠CDF,即③正确;
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3×(﹣5)+(﹣32)÷(﹣4)
(2)
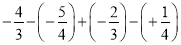
(3)
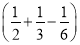 ×(﹣18)
×(﹣18)(4)﹣23÷
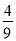 ×(﹣
×(﹣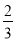 )2﹣|﹣2|
)2﹣|﹣2| -
科目: 来源: 题型:
查看答案和解析>>【题目】老师给同学们布置了一道社会实践题,收集并统计本地区一周内的最高气温和最低气温.小明根据收集到的数据列出了表格:
星期天
星期一
星期二
星期三
星期四
星期五
星期六
最高气温(℃)
+5
+6
+4
+1
+1
+3
+3
最低气温(℃)
+1
+3
+1
﹣3
﹣4
﹣3
﹣2
(1)本周内当地最高气温和最低气温分别是多少℃?
(2)在这一周中,哪一天的温差最大?最大温差是多少?
(3)这一周的最低气温的平均数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
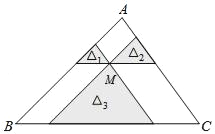
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校初三某班 50 名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如表所示:
自选项目
人数
频率
立定跳远
9
0.18
三级蛙跳
12
a
一分钟跳绳
8
0.16
投掷实心球
b
0.32
推铅球
5
0.10
合计
50
1
(1)填空:a= ,b= ;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“立定跳远”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有 3 名男生、2 名女生,为了了解学生的训练效果,从这 5 名学生中随机抽取两名学生进行推铅球测试,请用列表法或树形图法求所抽取的两名学生中至多有一名男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,正方形 OABC 的边 OA 在数轴上,O 为原点,正方形 OABC 的面积为 16.
(1)数轴上点 A 表示的数为 .
(2)将正方形 OABC 沿数轴水平移动,移动后的正方形记为O' A' B' C' ,移动后的正方形O' A' B' C ' 与原正方形 OABC 重叠部分的面积记为 S,如图 2 中,长方形O ' ABC ' 的面积为 S.当 S 恰好等于原正方形 OABC 面积的
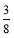 时,数轴上点A' 示的数为 .
时,数轴上点A' 示的数为 . (3)设点 A 的移动距离AA' = x,D 为线段AA' 的中点,点 E 在线段OO ' 上,且OE =
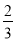 OO ' ,当OD + OE = 5 时,求x的值并写出此时点 A' 所对应的数.
OO ' ,当OD + OE = 5 时,求x的值并写出此时点 A' 所对应的数. 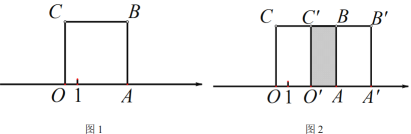
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=
 ,求BC的长.
,求BC的长.
【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵

∴

∴


点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22【题目】如图,一次函数y=k1x+b与反比例函数y=
 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>
 的解集;
的解集;(3)若P(p,y1),Q(﹣2,y2)是函数y=
 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.
相关试题

