【题目】如图1,在平面直角坐标系中,O是坐标原点,矩形OACB的顶点A、B分别在![]() 轴和
轴和![]() 轴上,已知OA=5,OB=3,点D的坐标是(0,1),点P从点B出发以每秒1个单位的速度沿折线BCA的方向运动,当点P与点A重合时,运动停止,设运动的时间为
轴上,已知OA=5,OB=3,点D的坐标是(0,1),点P从点B出发以每秒1个单位的速度沿折线BCA的方向运动,当点P与点A重合时,运动停止,设运动的时间为![]() 秒.
秒.

(1)点P运动到与点C重合时,求直线DP的函数解析式;
(2)求△OPD的面积S关于![]() 的函数解析式,并写出对应
的函数解析式,并写出对应![]() 的取值范围;
的取值范围;
(3)点P在运动过程中,是否存在某些位置使△ADP是不以DP为底边的等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)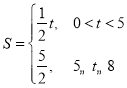 ;(3)存在满足条件的点P,其坐标为
;(3)存在满足条件的点P,其坐标为![]() 或
或![]() 或
或![]()
【解析】
(1)先求出C点坐标,然后用待定系数法求直线DP的解析式即可;
(2)分点P在线段BC上和在线段AC上两种情况,分别求得s关于的函数解析式;
(3)当点P在线段BC上时,可用t表示出点P点坐标,再分别表示出DP、AP和AD的长,然后再分DP=AP、DP=AD和AP=AD三种情况分别求得关于t的方程,即可求得P点的坐标;当点P在线段AC上时,则只能有PD=AD,则点D在线段AP的垂直平分线上,即可确定线段AP中点的坐标,从而可求得P点坐标.
解:(1)![]() ,
,![]() ,且四边形
,且四边形![]() 为长方形,
为长方形,
![]() ,
,
∴当点P与点C重合时,P点坐标为![]() ,
,
设直线DP解析式为![]() ,
,
![]() ,解得
,解得![]() ,
,
直线DP解析式为![]() .
.
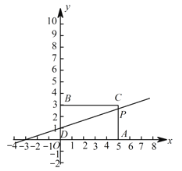
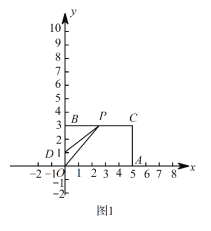
(2)当![]() 时,如图1,
时,如图1,
则![]() ,且
,且![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
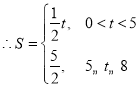 .存在满足条件的点P,其坐标为
.存在满足条件的点P,其坐标为![]() 或
或![]() 或
或![]()
(3)存在,理由如下:
当点P在线段BC上时,如图2,

设P点坐标为![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∵△ADP是不以DP为底边的等腰三角形
∴有![]() ,
,![]() 两种情况,
两种情况,
①当![]() 时,则有
时,则有![]() ,解得
,解得![]() ,此时P点坐标为
,此时P点坐标为![]() ;
;
②当![]() 时,则有
时,则有![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() ,此时P点坐标为
,此时P点坐标为![]() ;
;
当点P在线段AC上时,
![]() ,
,
∴只有![]() ,
,
![]() 在线段
在线段![]() 的垂直平分线上,
的垂直平分线上,
∴线段![]() 的中点坐标为
的中点坐标为![]() ,
,
∴P点坐标为![]() ;
;
综上可知存在满足条件的点P,其坐标为![]() 或
或![]() 或
或![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条直线经过点A(5,0),B(1,4).
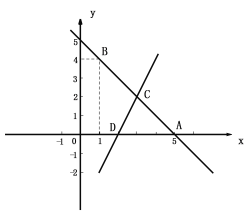
(1)求直线AB的解析式;
(2)若直线
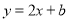 与直线AB相交于点C(3,
与直线AB相交于点C(3,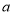 ),与
),与 轴相交于点D,求
轴相交于点D,求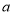 、
、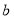 的值以及△ACD的面积.
的值以及△ACD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔赛跑”的故事同学们非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列的问题:
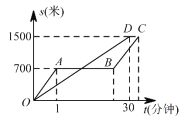
(1)折线OABC表示赛跑过程中__________(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全程是_________米;
(2)乌龟用了多少分钟追上正在睡觉的兔子?
(3)兔子醒来,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你计算兔子中间睡觉用了多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC=8,点D在△ABC外,连接AD、BD,且∠ADB=90°,AB、CD相交于点E,AB、CD的中点分别是点F、G,连接FG.

(1)求AB的长;
(2)求证:AD+BD=
 CD;
CD;(3)若BD=6,求FG的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系xOy中,线段BC∥x轴、线段AB∥y轴,点B坐标为(4,3),反比例函数y=
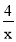 (x>0)的图像与线段AB交于点D,与线段BC交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,则点B'的纵坐标是( )
(x>0)的图像与线段AB交于点D,与线段BC交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,则点B'的纵坐标是( )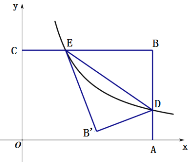
A.
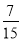 B.
B.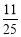 C.
C.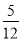 D.
D.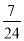
相关试题

