【题目】“龟兔赛跑”的故事同学们非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列的问题:
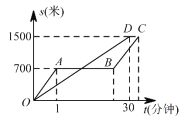
(1)折线OABC表示赛跑过程中__________(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全程是_________米;
(2)乌龟用了多少分钟追上正在睡觉的兔子?
(3)兔子醒来,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你计算兔子中间睡觉用了多少分钟?
参考答案:
【答案】(1)兔子,1500;(2)14分钟;(3)27.5分钟
【解析】
(1)利用乌龟始终运动,中间没有停留,进而得出线段OABC的意义和全程的距离;
(2)根据乌龟所走路程除以所用时间即可解答;
(4)用乌龟跑完全程的时间-兔子晚到的时间-兔子在路上奔跑的两端所用时间即可解答.
解:(1)![]() 龟始终运动,中间没有停留
龟始终运动,中间没有停留
![]() 折线OABC表示赛跑过程中兔子的路程与时间的关系,
折线OABC表示赛跑过程中兔子的路程与时间的关系,
由图可知,赛跑的全程是1500米;
故答案为:兔子,1500米;
(2)∵乌龟的速度是:1500÷30=50米/分钟
∴700÷50=14分钟
答:乌龟用了14分钟追上正在睡觉的兔子;
(3)∵兔子睡醒后跑向终点所用的时间:(1500-700)÷400=2分钟;
∴兔子中间睡觉的时间是:30+0.5-2-1=27.5分钟.
答:兔子中间睡觉用了27.5分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班在甲、乙两名同学中选拔一人参加学校数学竞赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
次数
1
2
3
4
5
甲
79
86
82
85
83
乙
88
79
90
81
77
回答下列问题:
(1)请分别求出甲、乙两同学测试成绩的平均数;
(2)经计算知
 ,
, ,你认为选拔谁参加比赛更合适,说明理由.
,你认为选拔谁参加比赛更合适,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业在“蜀南竹海”收购毛竹,直接销售,每吨可获利100元,进行粗加工,每天可加工8吨,每吨可获利800元;如果对毛竹进行精加工,每天可加工1吨,每吨可获利4000元.由于受条件限制,每天只能采用一种方式加工,要求将在一月内(30天)将这批毛竹93吨全部销售.为此企业厂长召集职工开会,让职工讨论如何加工销售更合算.
甲说:将毛竹全部进行粗加工后销售;
乙说:30天都进行精加工,未加工的毛竹直接销售;
丙说:30天中可用几天粗加工,再用几天精加工后销售;
请问厂长应采用哪位说的方案做,获利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条直线经过点A(5,0),B(1,4).
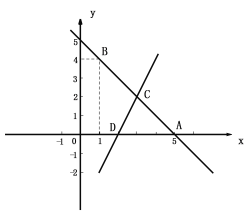
(1)求直线AB的解析式;
(2)若直线
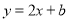 与直线AB相交于点C(3,
与直线AB相交于点C(3,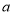 ),与
),与 轴相交于点D,求
轴相交于点D,求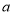 、
、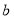 的值以及△ACD的面积.
的值以及△ACD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,O是坐标原点,矩形OACB的顶点A、B分别在
 轴和
轴和 轴上,已知OA=5,OB=3,点D的坐标是(0,1),点P从点B出发以每秒1个单位的速度沿折线BCA的方向运动,当点P与点A重合时,运动停止,设运动的时间为
轴上,已知OA=5,OB=3,点D的坐标是(0,1),点P从点B出发以每秒1个单位的速度沿折线BCA的方向运动,当点P与点A重合时,运动停止,设运动的时间为 秒.
秒.
(1)点P运动到与点C重合时,求直线DP的函数解析式;
(2)求△OPD的面积S关于
 的函数解析式,并写出对应
的函数解析式,并写出对应 的取值范围;
的取值范围;(3)点P在运动过程中,是否存在某些位置使△ADP是不以DP为底边的等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC=8,点D在△ABC外,连接AD、BD,且∠ADB=90°,AB、CD相交于点E,AB、CD的中点分别是点F、G,连接FG.

(1)求AB的长;
(2)求证:AD+BD=
 CD;
CD;(3)若BD=6,求FG的值.
相关试题

